
【题目】在△ABC中,a、b、c分别是角A、B、C的对边,且 ![]() ,
,
(1)求角B的大小;
(2)若 ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:由正弦定理 ![]() 得:
得:
a=2RsinA,b=2RsinB,c=2RsinC,
将上式代入已知 ![]() ,
,
即2sinAcosB+sinCcosB+cosCsinB=0,
即2sinAcosB+sin(B+C)=0,
∵A+B+C=π,
∴sin(B+C)=sinA,
∴2sinAcosB+sinA=0,即sinA(2cosB+1)=0,
∵sinA≠0,∴ ![]() ,
,
∵B为三角形的内角,∴ ![]()
(2)解:将 ![]() 代入余弦定理b2=a2+c2﹣2accosB得:
代入余弦定理b2=a2+c2﹣2accosB得:
b2=(a+c)2﹣2ac﹣2accosB,即 ![]() ,
,
∴ac=3,
∴ ![]()
【解析】(1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出b2,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中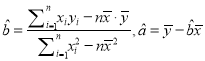 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段![]() 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求第四小组的频率,并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是![]() ~
~![]() 分及
分及![]() ~
~![]() 分的学生中选两人,记他们的成绩为
分的学生中选两人,记他们的成绩为![]() ,求满足“
,求满足“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点为极点,
),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)讨论直线![]() 与圆
与圆![]() 的公共点个数;
的公共点个数;
(Ⅱ)过极点作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求点
,求点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长.
相交所得弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() 三所高校,其学生会学习部有“干事”人数分别为
三所高校,其学生会学习部有“干事”人数分别为![]() ,现采用分层抽样的方法从这些“干事”中抽取
,现采用分层抽样的方法从这些“干事”中抽取![]() 名进行“大学生学习部活动现状”调查.
名进行“大学生学习部活动现状”调查.
(1)求应从![]() 这三所高校中分别抽取的“干事”人数;
这三所高校中分别抽取的“干事”人数;
(2)若从抽取的![]() 名干事中随机选两名干事,求选出的
名干事中随机选两名干事,求选出的![]() 名干事来自同一所高校的概率.
名干事来自同一所高校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为a1= ![]() ,且2an+1=an(n∈N+).
,且2an+1=an(n∈N+).
(1)求{an}的通项公式;
(2)若数列{bn}满足bn= ![]() ,求{bn}的前n项和Tn .
,求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=![]() ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com