
【题目】某公司招聘员工,先由两位专家面试,若两位专家都同意通过,则视作通过初审予以录用;若这两位专家都未同意通过,则视作未通过初审不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为![]() ,复审能通过的概率为
,复审能通过的概率为![]() ,各专家评审的结果相互独立.
,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率;
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
科目:高中数学 来源: 题型:
【题目】圆周上有![]() 个点
个点![]() ,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为
,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为![]() .
.
(1).直接画图求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2).确定![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学基本公式大赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
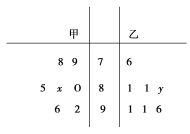
(1)求x和y的值;
(2)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为![]() ,容积为
,容积为![]() .
.
(1)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(2)求当![]() 为多少时,容器的容积最大?并求出最大容积.
为多少时,容器的容积最大?并求出最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设整数![]() ,对置于
,对置于![]() 个点
个点![]() 及点
及点![]() 处的卡片作如下操作:操作
处的卡片作如下操作:操作![]() :若某个点
:若某个点![]() 处的卡片数不少于3,则可从中取出三张,在三点
处的卡片数不少于3,则可从中取出三张,在三点![]() 、
、![]() 、
、![]() 处各放一张
处各放一张![]() ;操作
;操作![]() :若点
:若点![]() 处的卡片数不少于
处的卡片数不少于![]() ,则可从中取出
,则可从中取出![]() 张,在
张,在![]() 个点
个点![]() 处各放一张。证明:只要放置于这
处各放一张。证明:只要放置于这![]() 个点处的卡片总数不少于
个点处的卡片总数不少于![]() ,则总能通过若干次操作,使得每个点处的卡片数均不少于
,则总能通过若干次操作,使得每个点处的卡片数均不少于![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4,5这六个数字,完成下面三个小题.
(1)若数字允许重复,可以组成多少个不同的五位偶数;
(2)若数字不允许重复,可以组成多少个能被5整除的且百位数字不是3的不同的五位数;
(3)若直线方程![]() 中的a,b可以从已知的六个数字中任取2个不同的数字,则直线方程表示的不同直线共有多少条?
中的a,b可以从已知的六个数字中任取2个不同的数字,则直线方程表示的不同直线共有多少条?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com