
【题目】圆![]() 内有一点P(-1,2),AB为过点P且倾斜角为
内有一点P(-1,2),AB为过点P且倾斜角为![]() 的弦.
的弦.
(1)当![]() 时,求AB的长;
时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
【答案】(1)(6′)依题意直线AB的斜率为-1,直线AB的方程为:y-2=-(x+1),圆心O(0,0)到直线AB的距离为d=![]() ,则
,则![]() AB
AB![]() =
=![]() =
=![]() ,
,![]() AB的长为
AB的长为![]() .
.
(2)(6′)当弦AB被点P平分时,弦AB与OP垂直,此时OP的斜率为-2,所以AB的斜率为![]() ,根据点斜式方程直线AB的方程为x-2y+5=0.
,根据点斜式方程直线AB的方程为x-2y+5=0.
【解析】
(1)过点O做OG⊥AB于G,连接OA,依题意可知直线AB的斜率,求得AB的
方程,利用点到直线的距离求得OG,由圆的半径进而求得OA的长,则OB可求得;
(2)弦AB被P平分时,OP⊥AB,则OP的斜率可知,利用点斜式求得AB的方程.
(1) 过点O做OG⊥AB于G,连接OA;过点P(-1,2)的直线AB倾斜角![]()
直线AB斜率-1,则直线AB的方程是:y=-x+1
![]()
![]() 圆的半径
圆的半径![]()

(2))当弦被点P平分时,![]() 此时直线OP的斜率-2,
此时直线OP的斜率-2,
则直线AB的斜率为![]() ,
,
由直线的点斜式方程可知,直线AB的方程为:![]()
即直线AB的方程为:x-2y+5 =0


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() ,若将
,若将![]() 沿
沿![]() 折起,得到几何体
折起,得到几何体![]() .
.
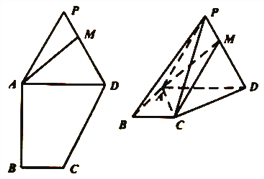
(1)试问:直线![]() 与平面
与平面![]() 是否有公共点?并说明理由;
是否有公共点?并说明理由;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
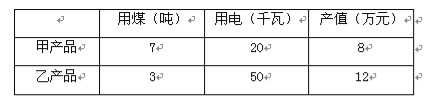
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点P(1,
,点P(1,![]() )在椭圆C上,直线l过椭圆的右焦点与椭圆相交于A,B两点.
)在椭圆C上,直线l过椭圆的右焦点与椭圆相交于A,B两点.
(1)求椭圆C的方程;
(2)在x轴上是否存在定点M,使得![]() 为定值?若存在,求定点M的坐标;若不在,请说明理由.
为定值?若存在,求定点M的坐标;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边的中点,现把
边的中点,现把![]() 沿
沿![]() 折叠,使其与
折叠,使其与![]() 构成如图2所示的三棱锥
构成如图2所示的三棱锥![]() ,且
,且![]() .
.
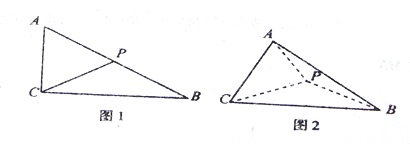
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 夹角的余弦值.
夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累积答对3题或打错3题即终止其初赛的比赛:答对3题者直接进入初赛,打错3题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为![]() .
.
(1)求选手甲可进入决赛的概率.
(2)设选手甲在初赛中答题的个数为![]() ,试求
,试求![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C中心在原点,焦点在x轴上,左右焦点分别为F1,F2,且|F1F2|=2,点(1,![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程.
,求以F2为圆心且与直线l相切的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com