
两点等分单位圆时,有相应正确关系为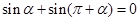 ;三点等分单位圆时,有相应正确关系为
;三点等分单位圆时,有相应正确关系为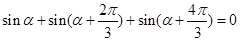 。由此可以推知:四点等分单位圆时的相应正确关系为
。由此可以推知:四点等分单位圆时的相应正确关系为

【解析】
试题分析:用两点等分单位圆时,关系为sinα+sin(π+α)=0,两个角的正弦值之和为0,且第一个角为α,第二个角与第一个角的差为:(π+α)-α=π,
用三点等分单位圆时,关系为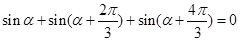 ,此时三个角的正弦值之和为0,且第一个角为α,第二个角与第一个角的差与第三个角与第二个角的差相等,均为有(
,此时三个角的正弦值之和为0,且第一个角为α,第二个角与第一个角的差与第三个角与第二个角的差相等,均为有(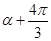 )-(
)-(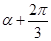 )=(
)=(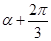 )-α=
)-α=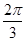 .
.
依此类推,可得当四点等分单位圆时,为四个角正弦值之和为0,且第一个角为α,第二个角为
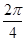 +α=
+α=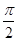 +α,第三个角
+α,第三个角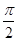 +α+
+α+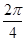 =π+α,第四个角为π+α+
=π+α,第四个角为π+α+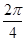 =
=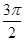 +α,
+α,
即其关系为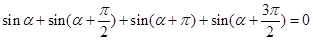 。
。
考点:本题主要考查归纳推理。
点评:中档题,解题的关键在于分析两点等分单位圆与三点等分单位圆的正弦值的个数及角的关系,归纳得出关系式变化的规律。


科目:高中数学 来源: 题型:
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
运用物理中矢量运算及向量坐标表示与运算,我们知道:
(1)若两点等分单位圆时,有相应关系为:![]() (2)四点等分单位圆时,有相应关系为:
(2)四点等分单位圆时,有相应关系为:
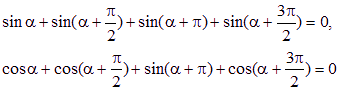
由此可以推知三等分单位圆时的相应关系为:
查看答案和解析>>
科目:高中数学 来源:2014届湖北稳派教育高三10月联合调研考试理科数学试卷(解析版) 题型:填空题
运用物理中矢量运算及向量坐标表示与运算,我们知道:两点等分单位圆时,有相应正确关系为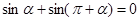 ,三等分单位圆时,有相应正确关系为
,三等分单位圆时,有相应正确关系为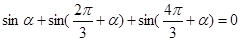 ,由此推出:四等分单位圆时的相应正确关系为
.
,由此推出:四等分单位圆时的相应正确关系为
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第四次月考理科数学试卷 题型:填空题
两点等分单位圆时,有相应正确关系为: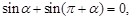 三点等分单位圆时,有相应正确关系为:
三点等分单位圆时,有相应正确关系为: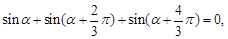 由此可以推知四点等分单位圆时的相应正确关系为__________
由此可以推知四点等分单位圆时的相应正确关系为__________
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三上学期期中考试数学理卷 题型:填空题
两点等分单位圆时,有相应正确关系为: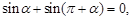 三点等分单位圆时,有相应正确关系为:
三点等分单位圆时,有相应正确关系为: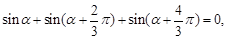 由此可以推知四点等分单位圆时的相应正确关系为
.
由此可以推知四点等分单位圆时的相应正确关系为
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com