
【题目】已知各项均为正整数的数列{an}的前n项和为Sn,满足:Sn﹣1+kan=tan2﹣1,n≥2,n∈N*(其中k,t为常数).
(1)若k=![]() ,t=
,t=![]() ,数列{an}是等差数列,求a1的值;
,数列{an}是等差数列,求a1的值;
(2)若数列{an}是等比数列,求证:k<t.
【答案】(1)a1=1+![]() ,(2)见解析
,(2)见解析
【解析】
(1)由k=![]() ,t=
,t=![]() ,可得
,可得![]() (n≥2),设等差数列{an}的公差为d,分别令n=2,n=3,利用等差数列的性质即可得出.
(n≥2),设等差数列{an}的公差为d,分别令n=2,n=3,利用等差数列的性质即可得出.
(2)令公比为q>0,则an+1=anq,利用递推关系可得1=(q﹣1)[tan(q+1)﹣k],易知q≠1,从而可得t=0,从而证明.
(1)∵k=![]() ,t=
,t=![]() ,∴
,∴![]() (n≥2),设等差数列{an}的公差为d,
(n≥2),设等差数列{an}的公差为d,
令n=2,则![]() ,令n=3,则
,令n=3,则![]() ,
,
两式相减可得:![]() ,∵an>0,∴a3﹣a2=2=d.
,∵an>0,∴a3﹣a2=2=d.
由![]() ,且d=2,化为
,且d=2,化为![]() ﹣4=0,a1>0.
﹣4=0,a1>0.
解得a1=1+![]() .
.
(2)∵Sn﹣1+kan=tan2﹣1①,n≥2,n∈N*,所以Sn+kan+1=![]() ﹣1②,
﹣1②,
②-①得an+kan+1﹣kan=![]() ﹣
﹣![]() ,∴an=(an+1﹣an)[t(an+1+an)﹣k],
,∴an=(an+1﹣an)[t(an+1+an)﹣k],
令公比为q>0,则an+1=anq,∴(q﹣1)k+1=tan(q2﹣1),
∴1=(q﹣1)[tan(q+1)﹣k];∵对任意n≥2,n∈N*,
1=(q﹣1)[tan(q+1)﹣k]成立;∴q≠1,∴an不是一个常数;
∴t=0,∴Sn﹣1+kan=﹣1,且{an}是各项均为正整数的数列,∴k<0,
故k<t.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() :
: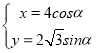 (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 是曲线
是曲线![]() 的左、右焦点,以原点
的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴且取相同单位长度建立极坐标系.
轴的非负半轴为极轴且取相同单位长度建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,![]() 为直线l上一点,求
为直线l上一点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】启东市政府拟在蝶湖建一个旅游观光项目,设计方案如下:如图所示的圆O是圆形湖的边界,沿线段AB,BC,CD,DA建一个观景长廊,其中A,B,C,D是观景长廊的四个出入口且都在圆O上,已知:BC=12百米,AB=8百米,在湖中P处和湖边D处各建一个观景亭,且它们关于直线AC对称,在湖面建一条观景桥APC.观景亭的大小、观景长廊、观景桥的宽度均忽略不计,设![]() .
.
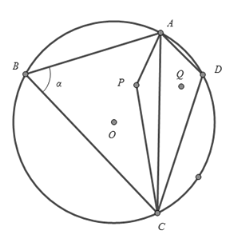
(1)若观景长廊AD=4百米,CD=AB,求由观景长廊所围成的四边形ABCD内的湖面面积;
(2)当![]() 时,求三角形区域ADC内的湖面面积的最大值;
时,求三角形区域ADC内的湖面面积的最大值;
(3)若CD=8百米且规划建亭点P在三角形ABC区域内(不包括边界),试判断四边形ABCP内湖面面积是否有最大值?若有,求出最大值,并写出此时![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,P为椭圆C上一点,且
,P为椭圆C上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]()
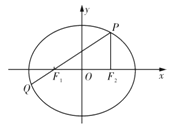
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围
的离心率的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人射击,甲射击一次中靶的概率是![]() ,乙射击一次中靶的概率是
,乙射击一次中靶的概率是![]() ,且
,且![]() 是方程
是方程![]() 的两个实根,已知甲射击5次,中靶次数的方差是
的两个实根,已知甲射击5次,中靶次数的方差是![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若两人各射击2次,至少中靶3次就算完成目标,则完成目标概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数不超过35人时,飞机票每张收费800元;若旅游团的人数多于35人,则给予优惠,每多1人,机票费每张减少10元,但旅游团的人数最多有60人.设旅行团的人数为![]() 人,飞机票价格为
人,飞机票价格为![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅游团的人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①函数![]() 的最大值为1;
的最大值为1;
②“若![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中所有正确命题的序号为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com