
 ,0),D(
,0),D( ,0),E(2,1),若使z取最大值时的最优解有无穷多个,则k= .
,0),E(2,1),若使z取最大值时的最优解有无穷多个,则k= .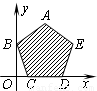
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
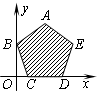 已知以x,y为自变量的目标函数z=kx+y (k>0)的可行域如图阴影部分(含边界),且A(1,2),B(0,1),C(
已知以x,y为自变量的目标函数z=kx+y (k>0)的可行域如图阴影部分(含边界),且A(1,2),B(0,1),C(| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 水是生命之源、生产之要、生态之基.2010年春季,西南5省面临世纪大旱,5000多万同胞受灾.这场少见的世纪大旱使农作物受灾面积近500万公顷,其中40万公顷良田颗粒无收,2000万同胞面临无水可饮的绝境.某乡镇对此次旱灾进行了认真的分析、总结,决定建造一个容积为4800m3,深为3m的长方体形无盖贮水池,以解决当地居民饮水、灌溉问题.已知贮水池池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底一边长为xm,总造价为y(单位:元).
水是生命之源、生产之要、生态之基.2010年春季,西南5省面临世纪大旱,5000多万同胞受灾.这场少见的世纪大旱使农作物受灾面积近500万公顷,其中40万公顷良田颗粒无收,2000万同胞面临无水可饮的绝境.某乡镇对此次旱灾进行了认真的分析、总结,决定建造一个容积为4800m3,深为3m的长方体形无盖贮水池,以解决当地居民饮水、灌溉问题.已知贮水池池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底一边长为xm,总造价为y(单位:元).查看答案和解析>>
科目:高中数学 来源:同步题 题型:填空题
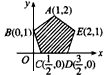
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com