
【题目】如图,三棱锥![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是
是![]() 的重心.
的重心.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且
,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于22℃.现有甲、乙、丙三地连续5天的日平均温度的记录数据:(记录数据都是正整数)
①甲地5个数据的中位数为24,众数为22;
②乙地5个数据的中位数为27,总体均值为24;
③丙地5个数据中有一个数据是32,总体均值为26,总体方差为10.8.
则肯定进入夏季的地区有_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按
依次按![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项循环地分为
项循环地分为![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列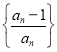 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com