
【题目】在直角坐标系xOy中,直线C的参数方程为![]() 为参数),曲线P在以该直角坐标系的原点O的为极点,x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0.
为参数),曲线P在以该直角坐标系的原点O的为极点,x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0.
(1)求直线C的普通方程和曲线P的直角坐标方程;
(2)设直线C和曲线P的交点为A、B,求|AB|.
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个 ![]() 列联表;
列联表;
(2)判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(b8)xaab,当x(,3)∪(2,+)时,f(x)<0.
(1)求f(x)的解析式;
(2)若不等式f(x)<m的解集为R,求m的取值范围;
(3) 求不等式f(x)<m+18的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:
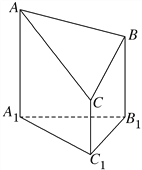
(Ⅰ)该几何体的体积;
(Ⅱ)截面ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
已知曲线C1的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在实数
,若存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“和有界数列”. 下列命题正确的是( )
为“和有界数列”. 下列命题正确的是( )
A. 若![]() 是等差数列,且首项
是等差数列,且首项![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
B. 若![]() 是等差数列,且公差
是等差数列,且公差![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
C. 若![]() 是等比数列,且公比
是等比数列,且公比![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
D. 若![]() 是等比数列,且
是等比数列,且![]() 是“和有界数列”,则
是“和有界数列”,则![]() 的公比
的公比![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com