
ЁОЬтФПЁПЦНаажОдИЭЖЕЕТМШЁФЃЪНЪЧИпПМжОдИЕФвЛжжаТЗНЪНЃЌ2008ФъНЬг§ВПдк6ИіЪЁЧјЪЕааЦНаажОдИЭЖЕЕТМШЁФЃЪНЕФЪдЕуИФИя.вЛФъЕФЪЕМљжЄпЖЃЌЪЕааЦНаажОдИЭЖЕЕТМШЁФЃЪНЃЌгааЇНЕЕЭСЫПМЩњжОдИЬюБЈЗчЯе.ЦНаажОдИЪЧетбљЙцЖЈЃКдкЭЌвЛХњДЮЩшжУМИИіжОдИЃЌЕБПМЩњЗжЪ§ДяЕНетМИИібЇаЃЬсЕЕЯпЪБЃЌБОХњДЮЕФжОдИвРДЮМьЫїТМШЁ.ФГПМЩњИљОнЖдздМКЕФИпПМЗжЪ§КЭЖдЭљФъбЇаЃТМШЁЧщПіЗжЮіЃЌДгБЈПМжИФЯжабЁдёСЫ10ЫљбЇаЃЃЌзїГіШчЯТБэИёЃК
бЇаЃ |
|
|
|
|
|
|
|
|
|
|
зЈвЕ | Ъ§бЇЯЕ | МЦЫуЛњЯЕ | ЮяРэЯЕ | |||||||
ТМШЁИХТЪ | 0.5 | 0.5 | 0.6 | 0.9 | 0.5 | 0.7 | 0.8 | 0.7 | 0.8 | 0.9 |
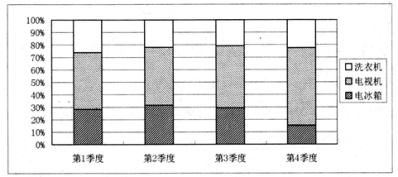
ЃЈ1ЃЉИУПМЩњДгЩЯБэжаЕФ10ЫљбЇаЃжабЁдё4ЫљбЇаЃЬюБЈЃЌМЧ![]() ЮЊбЁдёЕФ4ЫљбЇаЃжаБЈЪ§бЇЯЕзЈвЕЕФИіЪ§ЃЌЧѓ
ЮЊбЁдёЕФ4ЫљбЇаЃжаБЈЪ§бЇЯЕзЈвЕЕФИіЪ§ЃЌЧѓ![]() ЕФЗжВМСаМАЦфЦкЭћ
ЕФЗжВМСаМАЦфЦкЭћ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєИУПМЩњбЁдёСЫ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ет4ИібЇаЃдкЭЌвЛХњДЮЬюБЈжОдИЃЌЬюБЈжОдИБэШчЯТЃЌШчЙћНівдИУПМЩњЖдздМКЗжЮіЕФТМШЁИХТЪЮЊвРОнЃЌЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌЪЧЗёИФБфЫћБОХњДЮТМШЁЕФПЩФмадЃПЧыЫЕУїРэгЩ.
ет4ИібЇаЃдкЭЌвЛХњДЮЬюБЈжОдИЃЌЬюБЈжОдИБэШчЯТЃЌШчЙћНівдИУПМЩњЖдздМКЗжЮіЕФТМШЁИХТЪЮЊвРОнЃЌЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌЪЧЗёИФБфЫћБОХњДЮТМШЁЕФПЩФмадЃПЧыЫЕУїРэгЩ.
жОдИ | бЇаЃ |
ЕквЛжОдИ | |
ЕкЖўжОдИ | |
ЕкШ§жОдИ | |
ЕкЫФжОдИ |
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЈ2ЃЉВЛИФБфЫћБОХњДЮТМШЁЕФПЩФмадЃЌЯъМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнГЌМИКЮЗжВМЕФЗжВМСаКЭЪ§бЇЦкЭћМЦЫуЙЋЪНЃЌМЦЫуГіЗжВМСаКЭЪ§бЇЦкЭћ.
ЃЈ2ЃЉМЦЫуГіИУПМЩњдкБОХњДЮЮДБЛТМШЁЕФИХТЪЃЌгЩДЫХаЖЯГіЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌВЛИФБфЫћБОХњДЮТМШЁЕФПЩФмад.
ЃЈ1ЃЉ![]() ПЩФмШЁЕФжЕЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4
ПЩФмШЁЕФжЕЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЕФЗжВМСаЃК
ЕФЗжВМСаЃК
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]()
ЃЈ2ЃЉбЁдё![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ет4ИібЇаЃЕФИХТЪвРДЮЩшЮЊ
ет4ИібЇаЃЕФИХТЪвРДЮЩшЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ИУПМЩњдкБОХњДЮБЛТМШЁЕФИХТЪЮЊ
![]()
![]()
![]()
ЫљвдЃЌЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌВЛИФБфЫћБОХњДЮТМШЁЕФПЩФмад.
СэНтЃКИУПМЩњдкБОХњДЮЮДБЛТМШЁЕФИХТЪЮЊ![]()
ИУПМЩњдкБОХњДЮБЛТМШЁЕФИХТЪЮЊ![]()
ЫљвдЃЌЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌВЛИФБфЫћБОХњДЮТМШЁЕФПЩФмад.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛЦЌВњСПКмДѓЕФЫЎЙћжжжВдАЃЌдкСйНќГЩЪьЪБЫцЛњеЊЯТФГЦЗжжЫЎЙћ100ИіЃЌЦфжЪСПЃЈОљдкlжС11kgЃЉЦЕЪ§ЗжВМБэШчЯТЃЈЕЅЮЛ: kgЃЉЃК
Зжзщ | | | | | |
ЦЕЪ§ | 10 | 15 | 45 | 20 | 10 |
вдИїзщЪ§ОнЕФжаМфжЕДњБэетзщЪ§ОнЕФЦНОљжЕЃЌНЋЦЕТЪЪгЮЊИХТЪ.
ЃЈ1ЃЉгЩжжжВОбщШЯЮЊЃЌжжжВдАФкЕФЫЎЙћжЪСП![]() НќЫЦЗўДге§ЬЌЗжВМ
НќЫЦЗўДге§ЬЌЗжВМ![]() ЃЌЦфжа
ЃЌЦфжа![]() НќЫЦЮЊбљБОЦНОљЪ§
НќЫЦЮЊбљБОЦНОљЪ§![]() НќЫЦЮЊбљБОЗНВю
НќЫЦЮЊбљБОЗНВю![]() .ЧыЙРЫуИУжжжВдАФкЫЎЙћжЪСПдк
.ЧыЙРЫуИУжжжВдАФкЫЎЙћжЪСПдк![]() ФкЕФАйЗжБШЃЛ
ФкЕФАйЗжБШЃЛ
ЃЈ2ЃЉЯждкДгжЪСПЮЊ![]() ЕФШ§зщЫЎЙћжагУЗжВуГщбљЗНЗЈГщШЁ14ИіЫЎЙћЃЌдйДгет14ИіЫЎЙћжаЫцЛњГщШЁ3ИіЃЎШєЫЎЙћжЪСП
ЕФШ§зщЫЎЙћжагУЗжВуГщбљЗНЗЈГщШЁ14ИіЫЎЙћЃЌдйДгет14ИіЫЎЙћжаЫцЛњГщШЁ3ИіЃЎШєЫЎЙћжЪСП![]() ЕФЫЎЙћУПЯњЪлвЛИіЫљЛёЕУЕФЕФРћШѓЗжБ№ЮЊ2дЊЃЌ4дЊЃЌ6дЊЃЌМЧЫцЛњГщШЁЕФ3ИіЫЎЙћзмРћШѓЮЊ
ЕФЫЎЙћУПЯњЪлвЛИіЫљЛёЕУЕФЕФРћШѓЗжБ№ЮЊ2дЊЃЌ4дЊЃЌ6дЊЃЌМЧЫцЛњГщШЁЕФ3ИіЫЎЙћзмРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФЗжВМСаМАЪ§бЇЦкЭћ.
ЕФЗжВМСаМАЪ§бЇЦкЭћ.
ИНЃК![]()
![]() ЃЌдђ
ЃЌдђ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГЩЬГЁ2018ФъЯДвТЛњЁЂЕчЪгЛњКЭЕчБљЯфШ§жжЕчЦїИїМОЖШЯњСПЕФАйЗжБШЖбЛ§ЭМЃЈР§ШчЃКЕк3МОЖШФкЃЌЯДвТЛњЯњСПдМеМ![]() ЃЌЕчЪгЛњЯњСПдМеМ
ЃЌЕчЪгЛњЯњСПдМеМ![]() ЃЌЕчБљЯфЯњСПдМеМ
ЃЌЕчБљЯфЯњСПдМеМ![]() ЃЉ.ИљОнИУЭМЃЌвдЯТНсТлжавЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ
ЃЉ.ИљОнИУЭМЃЌвдЯТНсТлжавЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ
A. ЕчЪгЛњЯњСПзюДѓЕФЪЧЕк4МОЖШ
B. ЕчБљЯфЯњСПзюаЁЕФЪЧЕк4МОЖШ
C. ЕчЪгЛњЕФШЋФъЯњСПзюДѓ
D. ЕчБљЯфЕФШЋФъЯњСПзюДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШ§РтжљABCЉA1B1C1жаЃЌMЃЌM1ЗжБ№ЮЊABЃЌA1B1жаЕу.

ЃЈ1ЃЉЧѓжЄЃКC1M1ЁЮУцA1MCЃЛ
ЃЈ2ЃЉШєУцABCЁЭУцABB1A1ЃЌЁїAB1BЮЊе§Ш§НЧаЮЃЌABЃН2ЃЌBCЃН1ЃЌ![]() ЃЌЧѓЫФРтзЖB1ЉAA1C1CЕФЬхЛ§.
ЃЌЧѓЫФРтзЖB1ЉAA1C1CЕФЬхЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЪЧгЩе§ећЪ§зщГЩЕФЮоЧюЪ§Са.ШєДцдкГЃЪ§
ЪЧгЩе§ећЪ§зщГЩЕФЮоЧюЪ§Са.ШєДцдкГЃЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ШЮвтЕФ
ШЮвтЕФ![]() ГЩСЂЃЌдђГЦЪ§Са
ГЩСЂЃЌдђГЦЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() .
.
ЃЈ1ЃЉЗжБ№ХаЖЯЯТСаЪ§Са![]() ЪЧЗёОпгааджЪ
ЪЧЗёОпгааджЪ![]() ЃЛ (жБНгаДГіНсТл)
ЃЛ (жБНгаДГіНсТл)
Ђй![]()
Ђк![]()
ЃЈ2ЃЉШєЪ§Са![]() Тњзу
Тњзу![]() ЃЌЧѓжЄ:ЁАЪ§Са
ЃЌЧѓжЄ:ЁАЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() ЁБЪЧЁАЪ§Са
ЁБЪЧЁАЪ§Са![]() ЮЊГЃЪ§СаЁБЕФГфЗжБивЊЬѕМўЃЛ
ЮЊГЃЪ§СаЁБЕФГфЗжБивЊЬѕМўЃЛ
ЃЈ3ЃЉвбжЊЪ§Са![]() жа
жа![]() Чв
Чв![]() .ШєЪ§Са
.ШєЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪН.
ЕФЭЈЯюЙЋЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДѓздШЛЪЧЗЧГЃЦцУюЕФЃЌБШШчУлЗфНЈдьЕФЗфЗП.ЗфЗПЕФНсЙЙШчЭМЫљЪОЃЌПЊПкЮЊе§СљБпаЮABCDEFЃЌВрРтAA'ЁЂBB'ЁЂCC'ЁЂDD'ЁЂEE'ЁЂFF'ЯрЛЅЦНааЧвгыЦНУцABCDEFДЙжБЃЌЗфЗПЕзВПгЩШ§ИіШЋЕШЕФСтаЮЙЙГЩ.Ш№ЪПЪ§бЇМвПЫФсИёРћгУЮЂЛ§ЗжЕФЗНЗЈжЄУїСЫЗфЗПЕФетжжНсЙЙЪЧдкЯрЭЌШнЛ§ЯТЫљгУВФСЯзюЪЁЕФЃЌвђДЫЃЌгаШЫЫЕУлЗфБШШЫРрИќУїАзШчКЮгУЪ§бЇЗНЗЈЩшМЦздМКЕФМвдА.гЂЙњЪ§бЇМвТѓПЫРЭСжЭЈЙ§МЦЫуЕУЕНЁЯBЁфCЁфDЁфЃН109Ёу28Ёф16'.вбжЊвЛИіЗПжаBB'ЃН5![]() ЃЌABЃН2
ЃЌABЃН2![]() ЃЌtan54Ёу44Ёф08'
ЃЌtan54Ёу44Ёф08'![]() ЃЌдђДЫЗфЗПЕФБэУцЛ§ЪЧ_____.
ЃЌдђДЫЗфЗПЕФБэУцЛ§ЪЧ_____.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќЮхФъРДФГВнГЁбђжЛЪ§СПгыВнГЁжВБЛжИЪ§СНБфСПМфЕФЙиЯЕШчБэЫљЪОЃЌЛцжЦЯргІЕФЩЂЕуЭМЃЌШчЭМЫљЪОЃК
ФъЗн | 1 | 2 | 3 | 4 | 5 |
бђжЛЪ§СПЃЈЭђжЛЃЉ | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
ВнЕижВБЛжИЪ§ | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

ИљОнБэМАЭМЕУЕНвдЯТХаЖЯЃКЂйбђжЛЪ§СПгыВнГЁжВБЛжИЪ§ГЩМѕКЏЪ§ЙиЯЕЃЛЂкШєРћгУетЮхзщЪ§ОнЕУЕНЕФСНБфСПМфЕФЯрЙиЯЕЪ§ЮЊ![]() ЃЌШЅЕєЕквЛФъЪ§ОнКѓЕУЕНЕФЯрЙиЯЕЪ§ЮЊ
ЃЌШЅЕєЕквЛФъЪ§ОнКѓЕУЕНЕФЯрЙиЯЕЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂлПЩвдРћгУЛиЙщжБЯпЗНГЬЃЌзМШЗЕиЕУЕНЕБбђжЛЪ§СПЮЊ2ЭђжЛЪБЕФВнГЁжВБЛжИЪ§ЃЛвдЩЯХаЖЯжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЛЂлПЩвдРћгУЛиЙщжБЯпЗНГЬЃЌзМШЗЕиЕУЕНЕБбђжЛЪ§СПЮЊ2ЭђжЛЪБЕФВнГЁжВБЛжИЪ§ЃЛвдЩЯХаЖЯжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
A.0B.1C.2D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНx2+acosxЃЎ
ЃЈ1ЃЉЧѓКЏЪ§fЃЈxЃЉЕФЦцХМадЃЎВЂжЄУїЕБ|a|Ём2ЪБКЏЪ§fЃЈxЃЉжЛгавЛИіМЋжЕЕуЃЛ
ЃЈ2ЃЉЕБaЃНІаЪБЃЌЧѓfЃЈxЃЉЕФзюаЁжЕЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП11дТЃЌ2019ШЋЙњУРРіЯчДхРКЧђДѓШќдкжаЙњХЉДхИФИяЕФЗЂдДЕи-АВЛеЗябєОйАьЃЌЦфМфМзЁЂввСНШЫТжСїНјааРКЧђЖЈЕуЭЖРКБШШќЃЈУПШЫИїЭЖвЛДЮЮЊвЛТжЃЉЃЌдкЯрЭЌЕФЬѕМўЯТЃЌУПТжМзввСНШЫдкЭЌвЛЮЛжУЃЌМзЯШЭЖЃЌУПШЫЭЖвЛДЮЧђЃЌСНШЫга1ШЫУќжаЃЌУќжаепЕУ1ЗжЃЌЮДУќжаепЕУ-1ЗжЃЛСНШЫЖМУќжаЛђЖМЮДУќжаЃЌСНШЫОљЕУ0ЗжЃЌЩшМзУПДЮЭЖЧђУќжаЕФИХТЪЮЊ![]() ЃЌввУПДЮЭЖЧђУќжаЕФИХТЪЮЊ
ЃЌввУПДЮЭЖЧђУќжаЕФИХТЪЮЊ![]() ЃЌЧвИїДЮЭЖЧђЛЅВЛгАЯь.
ЃЌЧвИїДЮЭЖЧђЛЅВЛгАЯь.
ЃЈ1ЃЉОЙ§1ТжЭЖЧђЃЌМЧМзЕФЕУЗжЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаЃЛ
ЕФЗжВМСаЃЛ
ЃЈ2ЃЉШєОЙ§![]() ТжЭЖЧђЃЌгУ
ТжЭЖЧђЃЌгУ![]() БэЪООЙ§Ек
БэЪООЙ§Ек![]() ТжЭЖЧђЃЌРлМЦЕУЗжЃЌМзЕФЕУЗжИпгкввЕФЕУЗжЕФИХТЪ.
ТжЭЖЧђЃЌРлМЦЕУЗжЃЌМзЕФЕУЗжИпгкввЕФЕУЗжЕФИХТЪ.
ЂйЧѓ![]() ЃЛ
ЃЛ
ЂкЙцЖЈ![]() ЃЌОЙ§МЦЫуЛњМЦЫуПЩЙРМЦЕУ
ЃЌОЙ§МЦЫуЛњМЦЫуПЩЙРМЦЕУ![]() ЃЌЧыИљОнЂйжа
ЃЌЧыИљОнЂйжа![]() ЕФжЕЗжБ№аДГіaЃЌcЙигкbЕФБэДяЪНЃЌВЂгЩДЫЧѓГіЪ§Са
ЕФжЕЗжБ№аДГіaЃЌcЙигкbЕФБэДяЪНЃЌВЂгЩДЫЧѓГіЪ§Са![]() ЕФЭЈЯюЙЋЪН.
ЕФЭЈЯюЙЋЪН.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com