
 .
. 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件;
上递增的充分而不必要的条件;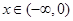 时,满足
时,满足 恒成立,求实数
恒成立,求实数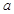 的取值范围.
的取值范围.
 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件,分为两步来证明先证明充分性,再证明不必要性。
上递增的充分而不必要的条件,分为两步来证明先证明充分性,再证明不必要性。 求导,得
求导,得  , …………2分
, …………2分 ,
, ,
, ,
,

 函数
函数 在区间
在区间 上递增. ……………4分
上递增. ……………4分 在区间
在区间 上递增, ∴
上递增, ∴ 对1<x<2恒成立
对1<x<2恒成立 得,
得, ,而
,而 ,
, ,即
,即 …………5分
…………5分 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件 ……7分
上递增的充分而不必要的条件 ……7分 ,令
,令 ,得
,得
 时不符合题意. …………8分
时不符合题意. …………8分 时,函数
时,函数 在(
在( )上递增,在
)上递增,在 上递减,
上递减, 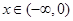 时,
时, 恒成立,需
恒成立,需 =
=
 6
6 ,得
,得 . …………………10分
. …………………10分 时,函数
时,函数 在(
在( )上递增,在
)上递增,在 上递减,
上递减,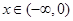 ,如满足
,如满足 恒成立,
恒成立,  得
得 …………12分
…………12分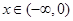 时,满足
时,满足 恒成立,实数
恒成立,实数


 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
 的定义域为(0,
的定义域为(0, ),且
),且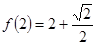 ,设点P是函数图象上的任意一点,过点P分别作直线
,设点P是函数图象上的任意一点,过点P分别作直线 和
和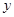 轴的垂线,垂足分别为M、N.
轴的垂线,垂足分别为M、N. 的值;
的值; 是否为定值?若是,则求出该定值,若不是,请说明理由;
是否为定值?若是,则求出该定值,若不是,请说明理由;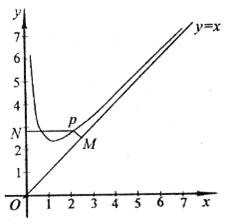
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com