
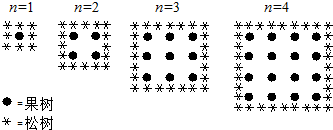 某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在如图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:
某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在如图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:分析 (1)由题意知,n=1时,果树1棵,松树9-1=8棵,n=2时,果树4棵,松树25-9=16棵,从而类比可得n=5时,果树25棵,松树121-81=40棵;从而可得${a_n}={n^2}$,bn=8n;
(2)化简${a_{n+1}}-{a_n}={({n+1})^2}-{n^2}=2n+1$,bn+1-bn=8(n+1)-8n=8,从而判断.
解答 解:(1)由题意知,
n=1时,果树1棵,松树9-1=8棵,
n=2时,果树4棵,松树25-9=16棵,
n=3时,果树9棵,松树49-25=24棵,
n=4时,果树16棵,松树81-49=32棵,
n=5时,果树25棵,松树121-81=40棵;
故${a_n}={n^2}$,bn=8n;
(2)${a_{n+1}}-{a_n}={({n+1})^2}-{n^2}=2n+1$,
bn+1-bn=8(n+1)-8n=8,
当n≤3时,2n+1<8,松树增加的速度快;
当n≥4时,2n+1>8,果树增加的速度快.
点评 本题考查了数列的应用及数列的增长速度的判断,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商品零售额 | 9.5 | 11.5 | 13.5 | 15.5 | 17.5 | 19.5 | 21.5 | 23.5 | 25.5 | 27.5 |
| 商品流通费率 | 6.0 | 4.6 | 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-1 | B. | 2$\sqrt{6}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com