
分析 进行对数的运算,从而得到f(x)=log22x-5log2x+6,可换元:令log2x=t,设y=f(x),从而可得到$y=(t-\frac{5}{2})^{2}-\frac{1}{4}$,从而根据t的范围,求该二次函数的值域即可得出原函数的值域.
解答 解:f(x)=(log2x-3)(log2x-2)=log22x-5log2x+6;
令log2x=t,0<t<2,设y=f(x),则:
$y={t}^{2}-5t+6=(t-\frac{5}{2})^{2}-\frac{1}{4}$,设y=g(t),则:
$g(\frac{5}{2})≤g(t)<g(1)$;
∴$-\frac{1}{4}≤g(t)<2$;
∴原函数的值域为$[-\frac{1}{4},2)$.
点评 考查函数值域的概念,对数的运算,换元法求函数的值域,以及配方求二次函数值域的方法.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
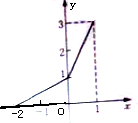 函数f(x)的图象是由两条线段组成的折线段(如图所示),则函数f(x)的表达式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.
函数f(x)的图象是由两条线段组成的折线段(如图所示),则函数f(x)的表达式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com