练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数f（x）=ln（x2﹣x）的定义域为（　　）
    A.（0，1）
    B.[0，1]
    C.（﹣∞，0）∪（1，+∞）
    D.（﹣∞，0]∪[1，+∞）

    【答案】C
    【解析】解：要使函数有意义，则x2﹣x＞0，即x＞1或x＜0，
    故函数的定义域为（﹣∞，0）∪（1，+∞），
    故选：C
    【考点精析】本题主要考查了函数的定义域及其求法的相关知识点，需要掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某地政府为了对房地产市场进行调控决策，统计部门对外来人口和当地人口进行了买房的心理预期调研，用简单随机抽样的方法抽取了110人进行统计，得到如下列联表（不全）：

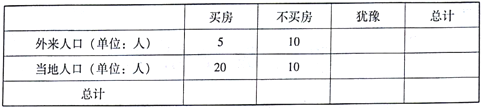
    已知样本中外来人口数与当地人口数之比为3:8.

    （1）补全上述列联表；

    （2）从参与调研的外来人口中用分层抽样方法抽取6人，进一步统计外来人口的某项收入指标，若一个买房人的指标记为3，一个犹豫人的指标记为2，一个不买房人的指标记为1，现在从这6人中再随机选取3人，求选取的3人的指标之和大于5的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2015 年 12 月，华中地区数城市空气污染指数“爆表”，此轮污染为 2015 年以来最严重的污染过程，为了探究车流量与的浓度是否相关，现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与的数据如表：

    时间

    星期一

    星期二

    星期三

    星期四

    星期五

    星期六

    星期日

    车流量（万辆）

    1

    2

    3

    4

    5

    6

    7

    的浓度（微克/立方米）

    28

    30

    35

    41

    49

    56

    62

    (1)由散点图知与具有线性相关关系，求关于的线性回归方程；（提示数据： ）

    (2)利用(1)所求的回归方程，预测该市车流量为 12 万辆时的浓度.

    参考公式：回归直线的方程是，

    其中.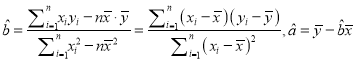

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面为平行四边形，平面平面， ,.

    （Ⅰ）求证: ；

    （Ⅱ）若三角形是边长为的等边三角形，求三棱锥外接球的表面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小型风力发电项目投资较少，开发前景广阔.受风力自然资源影响，项目投资存在一定风险.根据测算，IEC（国际电工委员会）风能风区的分类标准如下：

    风能分类

    一类风区

    二类风区

    平均风速m/s

    8.5---10

    6.5---8.5

    某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是：未来一年内，位于一类风区的A项目获利%的可能性为0.6，亏损%的可能性为0.4；

    B项目位于二类风区，获利35%的可能性为0.6，亏损10%的可能性是0.2，不赔不赚的可能性是0.2.

    假设投资A项目的资金为（）万元，投资B项目资金为（）万元，且公司要求对A项目的投资不得低于B项目.

    （Ⅰ）记投资A，B项目的利润分别为和，试写出随机变量与的分布列和期望， ;

    （Ⅱ）根据以上的条件和市场调研，试估计一年后两个项目的平均利润之和 的最大值，并据此给出公司分配投资金额建议.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下四个命题中正确的个数是（ ） （1.）若x∈R，则x2+ ≥x；
    （2.）若x≠kπ，k∈Z，则sinx+ ≥2；
    （3.）设x，y＞0，则 的最小值为8；
    （4.）设x＞1，则x+ 的最小值为3．
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，空间四边形ABCD中，AB=CD，AB⊥CD，E、F分别为BC、AD的中点，则EF和AB所成的角为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l：x+y﹣4=0，定点P（2，0），E，F分别是直线l和y轴上的动点，则△PEF的周长的最小值为（　　）
    A.2
    B.6
    C.3
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】今年入秋以来，某市多有雾霾天气，空气污染较为严重．市环保研究所对近期每天的空气污染情况进行调査研究后发现，每一天中空气污染指数与f（x）时刻x（时）的函数关系为f（x）=|log25（x+1）﹣a|+2a+1，x∈[0，24]，其中a为空气治理调节参数，且a∈（0，1）．
    （1）若a= ，求一天中哪个时刻该市的空气污染指数最低；
    （2）规定每天中f（x）的最大值作为当天的空气污染指数，要使该市每天的空气污染指数不超过3，则调节参数a应控制在什么范围内？

    查看答案和解析>>

    同步练习册答案