
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,若
,若![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程与离心率;
的方程与离心率;
(2)过点![]() 做直线
做直线![]() 与椭圆
与椭圆![]() 相交于两个不同的点
相交于两个不同的点![]() ;若
;若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】将正方体ABCD﹣A1B1C1D1沿三角形A1BC1所在平面削去一角可得到如图所示的几何体.
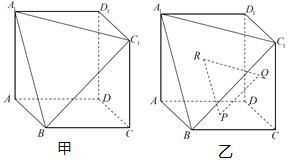
(1)连结BD,BD1,证明:平面BDD1⊥平面A1BC1;
(2)已知P,Q,R分别是正方形ABCDCDD1C1ADD1A1的中心(即对角线交点),证明:平面PQR∥平面A1BC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,题目是:“今有池方一丈,点生其中央,出水一尺,引葭赶岸,适马岸齐,问水深,葭长各几何?”题意是:有一正方形池塘,边长为一丈(10尺),有棵芦苇长在它的正中央,高出水面部分有1尺长,把芦苇拉向岸边,恰好碰到沿岸(池塘一边的中点),则水深为__________尺,芦苇长__________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆O:x2+y2=4上一动点,过点A作AB⊥x轴,垂足为B,动点D满足![]() .
.
(1)求动点D的轨迹C的方程;
(2)垂直于x轴的直线M交轨迹C于M、N两点,点P(3,0),直线PM与轨迹C的另一个交点为Q.问:直线NQ是否过一定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原来面积为![]() ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的![]() ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的![]() .
.
(1)到今年为止,该森林已砍伐了多少年?
(2)今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小
的距离小![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() .设线段
.设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com