练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     

    已知向量m＝（，），n＝(，)，记f(x)=m•n；

       （1）若f(x)=1,求的值；

       （2）若△ABC中，角A，B，C的对边分别是a,b,c，且满足（2a-c）cosB=bcosC，求函

            数f(A)的取值范围．

     

     

     

     

     

     

     

     

     

     

    【答案】

     解：（1）f(x)=m•n===，

          ∵f(x)=1，      ∴，              （…………4分）

          ∴=．            （…………6分）

        （2）∵（2a-c）cosB=bcosC，∴由正弦定理得，

         ∴，∴，

    ∵，∴，且，

    ∴   ∴；                      （…………10分）

    ∴，  ∴  ∴ ；

    又∵f(x)＝，∴f(A)=，（…………12分）

    故函数f(A)的取值范围是（1,）．               （…………14分）

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （09年临沂一模理）（12分）

    已知向量m＝（，1），n＝(，)。

    （I）                   若m•n=1,求的值;

    （II）               记f(x)=m•n，在△ABC中，角A，B，C的对边分别是a,b,c，且满足

    （2a-c）cosB=bcosC，求函数f(A)的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省高一暑假作业（六）必修4数学试卷（解析版） 题型：解答题

    已知向量m＝(sinA，cosA)，n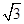＝(，－1)，m·n＝1，且A为锐角．

    (1)求角A的大小；

    (2)求函数f(x)＝cos2x＋4cosAsinx(x∈R)的值域．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年陕西省高三适应性考试理科数学试卷（解析版） 题型：解答题

    已知向量m＝（cosx，sinx），n＝（cosx，cosx）（x∈R），设函数f（x）＝m·n

    （1）求 f（x）的解析式，并求最小正周期．

    （2）若函数 g（x）的图像是由函数 f（x）的图像向右平移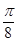个单位得到的，求g（x）的最大值及使g（x）取得最大值时x的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年陕西省高三适应性考试文科数学试卷（解析版） 题型：解答题

    已知向量m＝（cosx，sinx），n＝（cosx，cosx）（x∈R），设函数f（x）＝m·n

    （1）求 f（x）的解析式，并求最小正周期．

    （2）若函数 g（x）的图像是由函数 f（x）的图像向右平移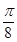个单位得到的，求g（x）的最大值及使g（x）取得最大值时x的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖南省长沙市高三第六次月考理科数学卷 题型：解答题

    (本小题满分12分)

    已知向量m＝(sin，1)，n＝(cos，cos2)，f(x)＝m·n.

    (1)若f(x)＝1，求cos(－x)的值；

    (2)在△ABC中，角A，B，C的对边分别是a，b，c且满足acosC＋c＝b，求函数f(B)的取值范围.

     

    查看答案和解析>>

    同步练习册答案