
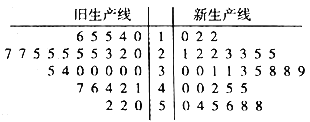
【题目】近几年,我国鲜切花产业得到了快速发展,相关部门制定了鲜切花产品行业等级标准,统一使用综合指标值![]() 进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
(Ⅰ)根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度(直接给出结论即可);
(Ⅱ)若从等级为三级的样品中随机选取3个进行生产流程调查,其中来自新型生产线的样品个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根据该花卉生产基地的生产记录,原有生产线加工的产品的单件平均利润为4元,产品的销售率(某等级产品的销量与产量的比值)及产品售价如下表:
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为10元,日产量3000件.因为鲜切花产品的保鲜特点,未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑,该生产基地是否需要引进该新型生产线?
【答案】(I)新型生产线综合指标值的平均值高于旧生产线的平均值,旧生产线的综合指标值相对来说更为集中;
(II)
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(III)该生产基地需要引进该新型生产线.
【解析】
(I)由茎叶图得新型生产线综合指标值的平均值高于旧生产线的平均值,旧生产线的综合指标值相对来说更为集中;
(II)由题意得等级为三级的样品共有8个,其中来自旧生产线的5个,新生产线的3个,随机变量X的取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列;
(Ⅲ)由茎叶图知该新型生产线加工的产品为三等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,一等品的概率
,一等品的概率![]() ,30000件产品中,三等品、二等品、一等品的件数的估计值分别为300件,1600件,1100件,求出单件产品利润,得到该生产基地需要引进新型生产线.
,30000件产品中,三等品、二等品、一等品的件数的估计值分别为300件,1600件,1100件,求出单件产品利润,得到该生产基地需要引进新型生产线.
(Ⅰ)由茎叶图可以看出,新型生产线综合指标值的平均值高于旧生产线的平均值;生产线的综合指标值相对于新型生产线来说更为集中.
(II)由題意可知,等级为三级的样品共有8个,其中来自旧生产线的5个,新生产线的3个,随机变量![]() 的取值为0,1,2,3,
的取值为0,1,2,3,
![]() ,
,
![]() ,
,
则![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
(Ⅲ)由茎叶图可知,该新型生产线加工的产品为三等品的概率![]() ,
,
二等品的概率![]() ,一等品的概率
,一等品的概率![]() ,
,
故3000件产品中,三等品、二等品、一等品的件数的估计值分别为300件,1600件,1100件,
三等品日销售总利润为![]() (元),
(元),
二等品日销售总利润为![]() (元),
(元),
一等品日销售总利润为![]() (元),
(元),
∴![]() (元).
(元).
故产品的单件平均利润的估计值为4.88元,高于4元,
综上,该生产基地需要引进该新型生产线.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】马林●梅森是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为了纪念梅森在数论方面的这一贡献,将形如2P﹣1(其中p是素数)的素数,称为梅森素数.若执行如图所示的程序框图,则输出的梅森素数的个数是( )
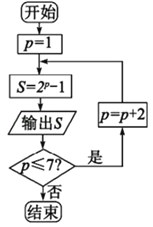
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
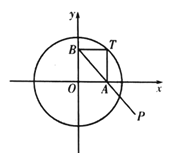
【题目】如图,点![]() 为圆
为圆![]() :
:![]() 上一动点,过点
上一动点,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() 延长至点
延长至点![]() ,使得
,使得![]() ,点
,点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,试问在曲线
,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线![]() 方程;若不存在,说明理由.
方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数
为函数![]() 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
①![]() ;②
;②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
(A)①②③ (B)②③ (C)①③ (D)②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,满足
,满足![]() .设
.设![]() 为
为![]() 上任一点,过
上任一点,过![]() 作
作![]() 的切线,其斜率
的切线,其斜率![]() 满足
满足![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() .设
.设![]() 为正常数.
为正常数.
①求![]() ;
;
②若不等式![]() 对任意的
对任意的![]() 恒成立,则实数
恒成立,则实数![]() 是否存在最大值?若存在,请求出这个值;若不存在,请说明理由.
是否存在最大值?若存在,请求出这个值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过点
)经过点![]() ,离心率为
,离心率为![]() ,
,![]() ,
,![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)求椭圆C的标准方程;
(2)若点![]() (
(![]() )在椭圆C上,求证;直线
)在椭圆C上,求证;直线![]() 与直线
与直线![]() 关于直线l:
关于直线l:![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com