
【题目】已知函数![]()
(1)讨论函数![]() 的单调区间.
的单调区间.
(2)设![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于区间[a,b](a<b),若函数![]() 同时满足:①
同时满足:①![]() 在[a,b]上是单调函数,②函数
在[a,b]上是单调函数,②函数![]() 在[a,b]的值域是[a,b],则称区间[a,b]为函数
在[a,b]的值域是[a,b],则称区间[a,b]为函数![]() 的“保值”区间
的“保值”区间
(1)求函数![]() 的所有“保值”区间
的所有“保值”区间
(2)函数![]() 是否存在“保值”区间?若存在,求
是否存在“保值”区间?若存在,求![]() 的取值范围,若不存在,说明理由
的取值范围,若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
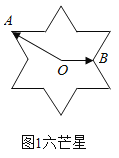
【题目】如图,“六芒星”是由两个全等正三角形组成,中心重合于点![]() 且三组对边分别平行,点
且三组对边分别平行,点![]() 是“六芒星”(如图)的两个顶点,动点
是“六芒星”(如图)的两个顶点,动点![]() 在“六芒星”上(内部以及边界),若
在“六芒星”上(内部以及边界),若![]() ,则
,则![]() 的取值可能是( )
的取值可能是( )
A.![]() B.1C.5D.9
B.1C.5D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ),且
),且![]() 的解集为
的解集为![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,满足
,满足![]() .
.
(1)求![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足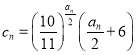 ,若
,若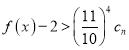 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有12支球队进行足球比赛,每两队都赛一场,胜者得3分,负者得0分,平局各得1分那么,有1支球队最少要得多少分才能保证最多有6支球队的得分不少于该队的得分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: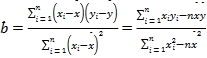 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com