
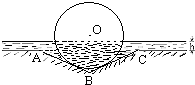
 (2012•徐汇区一模)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其它因素忽略不计).
(2012•徐汇区一模)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其它因素忽略不计).80
| ||
| 3 |
| 2×40 | ||
|
| 80 | ||
|
| 2×40 | ||
|
| 2×40 | ||
|
| 2×40 | ||
|
| 80 | ||
|
| 80 | ||
|


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
| am•an |
| 2 |
| 1 |
| m |
| 4 |
| n |
| 11 |
| 6 |
| 11 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com