
(本小题满分12分)
已知二项式 (
(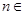 N*)展开式中,前三项的二项式系数和是
N*)展开式中,前三项的二项式系数和是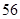 ,求:
,求:
(Ⅰ)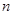 的值;
的值;
(Ⅱ)展开式中的常数项.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
设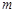 是给定的正整数,有序数组(
是给定的正整数,有序数组(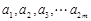 )中
)中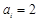 或
或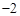
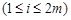 .
.
(1)求满足“对任意的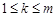 ,
,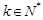 ,都有
,都有 ”的有序数组(
”的有序数组(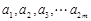 )的个数
)的个数 ;
;
(2)若对任意的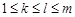 ,
,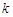 ,
, ,都有
,都有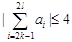 成立,求满足“存在
成立,求满足“存在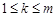 ,使得
,使得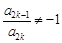 ”的有序数组(
”的有序数组(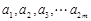 )的个数
)的个数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
规定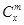 =
=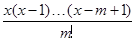 ,其中
,其中 是正整数,且
是正整数,且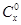 =1,这是组合数
=1,这是组合数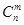 (
(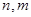 是正整数,且
是正整数,且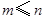 )的一种推广.
)的一种推广.
(1)求 的值;
的值;
(2)设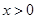 ,当
,当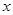 为何值时,
为何值时,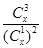 取得最小值?
取得最小值?
(3)组合数的两个性质:①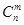 =
=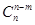 ; ②
; ②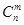 +
+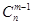 =
=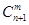
是否都能推广到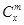 (
( 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球个数不少于白球个数的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7的取法
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
12月30日晚上,高二年级举行2011年元旦“师生红歌会”,某班有4名老师和4名学生站成一排。
(1)全部站成一排,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
(2)全部 站成一排,4名学生必须排在一起,共有多少种不同的排法?
站成一排,4名学生必须排在一起,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
(3)全部站成一排,任两名学生都不能相邻,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com