
【题目】已知点F1为椭圆![]() 的左焦点,
的左焦点,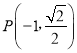 在椭圆上,PF1⊥x轴.
在椭圆上,PF1⊥x轴.
(1)求椭圆的方程:
(2)已知直线l与椭圆交于A,B两点,且坐标原点O到直线l的距离为![]() 的大小是否为定值?若是,求出该定值:若不是,请说明理由.
的大小是否为定值?若是,求出该定值:若不是,请说明理由.
【答案】(1)![]() y2=1;(2)∠AOB为定值
y2=1;(2)∠AOB为定值![]()
【解析】
(1)由PF1⊥x轴,及点P的坐标可得F1的坐标,即c的值,将P的坐标代入,由a,b,c之间的关系的关系求出a,b的值,进而求出椭圆的方程;
(2)分直线l的斜率存在和不存在两种情况讨论:当斜率不存在时由原点到直线的距离可得直线l的方程,代入椭圆中求出A,B的坐标,进而可得数量积![]() 的值为0,可得∠AOB
的值为0,可得∠AOB![]() ;当直线l的斜率存在时,设直线l的方程与椭圆联立求出两根之和及两根之积,由原点到直线的距离可得参数之间的关系,将其代入数量积
;当直线l的斜率存在时,设直线l的方程与椭圆联立求出两根之和及两根之积,由原点到直线的距离可得参数之间的关系,将其代入数量积![]() 的表达式,可得恒为0,即∠AOB恒为定值
的表达式,可得恒为0,即∠AOB恒为定值![]()
(1)因为PF1⊥x轴,又 在椭圆上,可得F1(﹣1,0),
在椭圆上,可得F1(﹣1,0),
所以c=1,![]() 1,a2=c2+b2,
1,a2=c2+b2,
解得a2=2,b2=1,
所以椭圆的方程为:![]() y2=1;
y2=1;
(2)当直线l的斜率不存在时,由原点O到直线l的距离为![]() ,
,
可得直线l的方程为:x![]() ,
,
代入椭圆可得A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )或A(
)或A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
可得![]() ,所以∠AOB
,所以∠AOB![]() ;
;
当直线l的斜率存在时,设直线的方程为:y=kx+m,设A(x1,y1),B(x2,y2),
由原点O到直线l的距离为![]() ,可得
,可得 ,可得3m2=2(1+k2),①
,可得3m2=2(1+k2),①
直线与椭圆联立 ,整理可得(1+2k2)x2+4kmx+2m2﹣2=0,
,整理可得(1+2k2)x2+4kmx+2m2﹣2=0,
![]() =16k2m2﹣4(1+2k2)(2m2﹣2)>0,将①代入
=16k2m2﹣4(1+2k2)(2m2﹣2)>0,将①代入![]() 中可得
中可得![]() =16m2+8>0,
=16m2+8>0,
x1+x2![]() ,x1x2
,x1x2![]() ,
,
y1y2=k2x1x2+km(x1+x2)+m2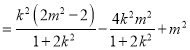
![]() ,
,
所以![]()
![]() ,
,
将①代入可得![]() 0,
0,
所以∠AOB![]() ;
;
综上所述∠AOB![]() 恒成立.
恒成立.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】刘徽是我国古代伟大的数学家,他的杰作《九章算术注》和《海岛算经》是我国最宝贵的数学遗产刘徽是世界上最早提出十进小数概念的人,他正确地提出了正负数的概念及其加减运算的规则.提出了“割圆术”,并用“割圆术”求出圆周率π为3.14.刘徽在割圆术中提出的“割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”被视为中国古代极限观念的佳作.其中“割圆术”的第一步是求圆的内接正六边形的面积,第二步是求圆的内接正十二边形的面积,依此类推.若在圆内随机取一点,则该点取自该圆内接正十二边形的概率为( )
A.![]() B.
B. C.
C.![]() D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系![]() 中,把到定点
中,把到定点![]() ,
,![]() 距离之积等于
距离之积等于![]() 的点的轨迹称为双纽线
的点的轨迹称为双纽线![]() .已知点
.已知点![]() 是双纽线
是双纽线![]() 上一点,下列说法中正确的有( )
上一点,下列说法中正确的有( )
①双纽线经过原点![]() ; ②双纽线
; ②双纽线![]() 关于原点
关于原点![]() 中心对称;
中心对称;
③![]() ; ④双纽线
; ④双纽线![]() 上满足
上满足![]() 的点
的点![]() 有两个.
有两个.
A.①②B.①②③C.②③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为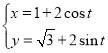 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求![]() ;
;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,直线
,直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,且
,且![]() 的面积不超过
的面积不超过![]() ,求直线
,求直线![]() 的倾斜角的取值范围.
的倾斜角的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
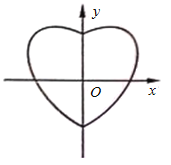
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com