
ЁОЬтФПЁПЮЊСЫНтЯВКУЬхг§дЫЖЏЪЧЗёгыадБ№гаЙиЃЌФГБЈМЧепЫцЛњВЩЗУ50ИіТЗШЫЃЌНЋЕїВщЧщПіНјааећРэКѓжЦГЩЯТБэЃК
ФъСфЃЈЫъЃЉ | [15ЃЌ25ЃЉ | [25ЃЌ35ЃЉ | [35ЃЌ45ЃЉ | [45ЃЌ55ЃЉ | [55ЃЌ65ЃЉ | [65ЃЌ75ЃЉ |
ЦЕЪ§ | 5 | 10 | 8 | 10 | 5 | 5 |
ЯВКУШЫЪ§ | 4 | 6 | 6 | 3 | 3 |
ЃЈ1ЃЉдкЕїВщЕФНсЙћжаЃЌЯВКУЬхг§дЫЖЏЕФХЎадга10ШЫЃЌВЛЯВКУЬхг§дЫЖЏЕФФаадга5ШЫЃЌЧыНЋЯТУцЕФ2ЁС2СаСЊБэВЙГфЭъећЃЌВЂХаЖЯФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.005ЕФЧАЬсЯТШЯЮЊЯВКУЬхг§дЫЖЏгыадБ№гаЙиЃПЫЕУїФуЕФРэгЩЃЛ
ЯВКУЬхг§дЫЖЏ | ВЛЯВКУЬхг§дЫЖЏ | КЯМЦ | |
ФаЩњ | 5 | ||
ХЎЩњ | 10 | ||
КЯМЦ | 50 |
ЃЈ2ЃЉШєДгФъСфдк[15ЃЌ25ЃЉЃЌ[25ЃЌ35ЃЉЕФБЛЕїВщепжаИїЫцЛњбЁШЁСНШЫНјаазЗзйЕїВщЃЌМЧбЁжаЕФ4ШЫжаВЛЯВКУЬхг§дЫЖЏЕФШЫЪ§ЮЊXЃЌЧѓЫцЛњБфСПXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ ЯТУцЕФСйНчжЕБэЙЉВЮПМЃК
PЃЈK2ЁнkЃЉ | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЃЈВЮПМЙЋЪНЃКK2= ![]() ЃЌЦфжаn=a+b+c+dЃЉ
ЃЌЦфжаn=a+b+c+dЃЉ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКИљОнЦЕТЪЗжВМБэжЊЃЌЯВКУЬхг§дЫЖЏЕФШЫЪ§ЮЊ30ЃЌдђВЛЯВКУЬхг§дЫЖЏЕФШЫЪ§ЮЊ20ЃЌ
ЬюаД2ЁС2СаСЊБэШчЯТЃК
ЯВКУЬхг§дЫЖЏ | ВЛЯВКУЬхг§дЫЖЏ | КЯМЦ | |
ФаЩњ | 20 | 5 | 25 |
ХЎЩњ | 10 | 15 | 25 |
КЯМЦ | 30 | 20 | 50 |
ИљОнСаСЊБэжаЪ§ОнЃЌМЦЫу
K2= ![]() =
= ![]() =3ЃМ7.879ЃЌ
=3ЃМ7.879ЃЌ
ЖдееСйНчжЕжЊЃЌдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.005ЕФЧАЬсЯТЃЌВЛФмШЯЮЊЯВКУЬхг§дЫЖЏгыадБ№гаЙиЃЛ
ЃЈ2ЃЉНтЃКДгФъСфдк[15ЃЌ25ЃЉЃЌ[25ЃЌ35ЃЉЕФБЛЕїВщепжаИїЫцЛњбЁШЁСНШЫНјаазЗзйЕїВщЃЌ
МЧбЁжаЕФ4ШЫжаВЛЯВКУЬхг§дЫЖЏЕФШЫЪ§ЮЊXЃЌ
вРЬтвтЕУX=0ЃЌ1ЃЌ2ЃЌ3ЃЌ
PЃЈX=0ЃЉ= ![]()
![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=1ЃЉ= ![]()
![]() +
+ ![]()
![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=2ЃЉ= ![]()
![]() +
+ ![]()
![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=3ЃЉ= ![]()
![]() =
= ![]() ЃЌ
ЃЌ
ЁрXЕФЗжВМСаЪЧЃК
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ЁрXЕФЪ§бЇЦкЭћEX=0ЁС ![]() +1ЁС
+1ЁС ![]() +2ЁС
+2ЁС ![]() +3ЁС
+3ЁС ![]() =
= ![]()
ЁОНтЮіЁПЃЈ1ЃЉИљОнЦЕТЪЗжВМБэЃЌМЦЫуЯВКУЬхг§дЫЖЏКЭВЛЯВКУЬхг§дЫЖЏЕФШЫЪ§ЃЌЬюаДСаСЊБэЃЌМЦЫуK2ЃЌЖдееСйНчжЕЕУГіНсТлЃЛЃЈ2ЃЉИљОнЬтвтжЊЫцЛњБфСПXЕФПЩФмШЁжЕЃЌМЦЫуЖдгІЕФИХТЪжЕЃЌаДГіЗжВМСаЃЌМЦЫуЪ§бЇЦкЭћжЕЃЎ


 ИїЕиЦкФЉИДЯАЬибЕОэЯЕСаД№АИ
ИїЕиЦкФЉИДЯАЬибЕОэЯЕСаД№АИ аЁВЉЪПЦкФЉДГЙи100ЗжЯЕСаД№АИ
аЁВЉЪПЦкФЉДГЙи100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдкRЩЯЕФПЩЕМКЏЪ§fЃЈxЃЉТњзуfЃЈxЃЉЉfЃЈЉxЃЉ=2x3 ЃЌ ЕБxЁЪЃЈЉЁоЃЌ0]ЪБf'ЃЈxЃЉЃМ3x2 ЃЌ ЪЕЪ§aТњзуfЃЈ1ЉaЃЉЉfЃЈaЃЉЁнЉ2a3+3a2Љ3a+1ЃЌдђaЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙХЯЃРАШЫГЃгУаЁЪЏзгдкЩГЬВЩЯАкГЩИїжжаЮзДРДбаОПЪ§ЃЎБШШчЃКЫћУЧбаОПЙ§ЭМЃЈ1ЃЉжаЕФ1,3,6,10ЃЌЁЃЌгЩгкетаЉЪ§ФмЙЛБэЪОГЩШ§НЧаЮЃЌЫљвдНЋЦфГЦЮЊШ§НЧаЮЪ§ЃЛРрЫЦЕиЃЌГЦЭМЃЈ2ЃЉжаЕФ1,4,9,16ЃЌЁетбљЕФЪ§ЮЊе§ЗНаЮЪ§ЃЎЯТСаЪ§жаМШЪЧШ§НЧаЮЪ§гжЪЧе§ЗНаЮЪ§ЕФЪЧЃЈ ЃЉ


A. 289 B. 1 024
C. 1 225 D. 1 378
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкжБНЧзјБъЯЕxOyжаЃЌЧњЯпC1ЕФВЮЪ§ЗНГЬЮЊ 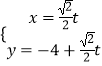 ЃЈtЮЊВЮЪ§ЃЉЃЌдкМЋзјБъЯЕЃЈвдзјБъдЕуOЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсЃЉжаЃЌЧњЯпC2ЕФЗНГЬЮЊІбsin2ІШ=2pcosІШЃЈpЃО0ЃЉЃЌЧњЯпC1ЁЂC2НЛгкAЁЂBСНЕуЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЌдкМЋзјБъЯЕЃЈвдзјБъдЕуOЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсЃЉжаЃЌЧњЯпC2ЕФЗНГЬЮЊІбsin2ІШ=2pcosІШЃЈpЃО0ЃЉЃЌЧњЯпC1ЁЂC2НЛгкAЁЂBСНЕуЃЎ
ЃЈЂёЃЉШєp=2ЧвЖЈЕуPЃЈ0ЃЌЉ4ЃЉЃЌЧѓ|PA|+|PB|ЕФжЕЃЛ
ЃЈЂђЃЉШє|PA|ЃЌ|AB|ЃЌ|PB|ГЩЕШБШЪ§СаЃЌЧѓpЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЪЧЖЈвхдкRЩЯЕФХМКЏЪ§ЃЌЧвдкЧјМф[0ЃЌ+ЁоЃЉЩЯЕЅЕїЕнМѕЃЌШєfЃЈlog2aЃЉ+fЃЈ3 ![]() aЃЉЁн2fЃЈЉ1ЃЉЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
aЃЉЁн2fЃЈЉ1ЃЉЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.[2ЃЌ4]
B.[ ![]() ЃЌ2]
ЃЌ2]
C.[ ![]() ЃЌ4]
ЃЌ4]
D.[ ![]() ЃЌ2]
ЃЌ2]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМЋЕугыжБНЧзјБъЯЕЕФдЕужиКЯЃЌМЋжсгыxжсЕФе§АыжсжиКЯЃЌдВCЕФМЋзјБъЪЧІб=2asinІШЃЌжБЯпlЕФВЮЪ§ЗНГЬЪЧ 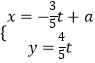 ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈ1ЃЉШєa=2ЃЌMЮЊжБЯпlгыxжсЕФНЛЕуЃЌNЪЧдВCЩЯвЛЖЏЕуЃЌЧѓ|MN|ЕФзюДѓжЕЃЛ
ЃЈ2ЃЉШєжБЯпlБЛдВCНиЕУЕФЯвГЄЮЊ ![]() ЃЌЧѓaЕФжЕЃЎ
ЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіДќзгРязАга7ИіЧђЃЌЦфжагаКьЧђ4ИіЃЌБрКХЗжБ№ЮЊ1ЃЌ2ЃЌ3ЃЌ4ЃЛАзЧђ3ИіЃЌБрКХЗжБ№ЮЊ2ЃЌ3ЃЌ4ЃЎДгДќзгжаШЮШЁ4ИіЧђЃЈМйЩшШЁЕНШЮКЮвЛИіЧђЕФПЩФмадЯрЭЌЃЉЃЎ
ЃЈЂёЃЉЧѓШЁГіЕФ4ИіЧђжаЃЌКЌгаБрКХЮЊ3ЕФЧђЕФИХТЪЃЛ
ЃЈЂђЃЉдкШЁГіЕФ4ИіЧђжаЃЌКьЧђБрКХЕФзюДѓжЕЩшЮЊXЃЌЧѓЫцЛњБфСПXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЩШаЮЕФжмГЄЮЊ30ЃЌЕБЫќЕФАыОЖRКЭдВаФНЧІСИїШЁКЮжЕЪБЃЌЩШаЮЕФУцЛ§SзюДѓЃПВЂЧѓГіЩШаЮУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХЉГЁЙВгаЭСЕи50ФЖЃЌетаЉЕиПЩжжЮїЙЯЁЂУоЛЈЁЂгёУзЃЎетаЉХЉзїЮяУПФЖЕиЫљашРЭСІКЭдЄМЦВњжЕШчЯТБэЃЎШєИУХЉГЁга20УћРЭЖЏСІЃЌгІдѕбљМЦЛЎВХФмЪЙУПФЖЕиЖМФмжжЩЯзїЮя(гёУзБижж)ЃЌЫљгаРЭЖЏСІЖМБЛАВХХЙЄзї(УПУћРЭЖЏСІжЛФмжжжВвЛжжзїЮя)ЧвзїЮядЄМЦзмВњжЕДязюИпЃП
зїЮя | РЭСІ/ФЖ | ВњжЕ/ФЖ |
ЮїЙЯ | 1/2 | 0.6ЭђдЊ |
УоЛЈ | 1/3 | 0.5ЭђдЊ |
гёУз | 1/4 | 0.3ЭђдЊ |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com