
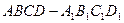 中,
中,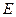 、
、 分别为棱
分别为棱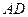 、
、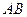 的中点.
的中点.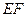 ∥平面
∥平面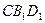 ;
;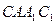 ⊥平面
⊥平面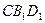 ;
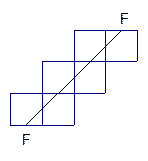
;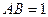 ,一个动点从点
,一个动点从点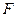 出发在正方体的
出发在正方体的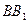 、
、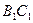 、
、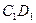 、
、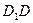 、
、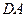 上的点,最终又回到点
上的点,最终又回到点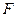 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.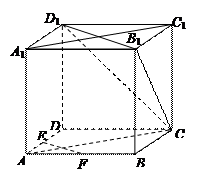
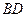 .
.
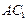 中,对角线
中,对角线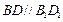 .
.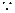 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,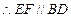 .
.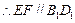 . …………2分
. …………2分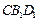 ,
,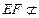 平面
平面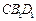 ,
, EF∥平面CB1D1. …………4分
EF∥平面CB1D1. …………4分 在正方体
在正方体 中,AA1⊥平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1, AA1⊥B1D1.
AA1⊥B1D1.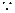 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,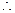 B1D1⊥平面CAA1C1. …………6分
B1D1⊥平面CAA1C1. …………6分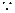 B1D1平面CB1D1,
B1D1平面CB1D1,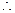 平面CAA1C1⊥平面CB1D1. …………8分
平面CAA1C1⊥平面CB1D1. …………8分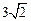 . …………9分
. …………9分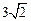 . …………12分.
. …………12分.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源:不详 题型:解答题
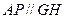
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
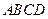 中,
中,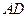 ∥
∥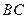 ,
,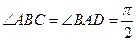 ,
,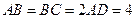 ,
, 、
、 分别是
分别是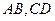 上的点,
上的点,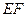 ∥
∥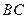 ,
,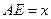 ,
,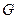 是
是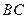 的中点。沿
的中点。沿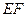 将梯形
将梯形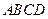 翻折,使平面
翻折,使平面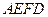 ⊥平面
⊥平面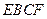 (如图) .
(如图) .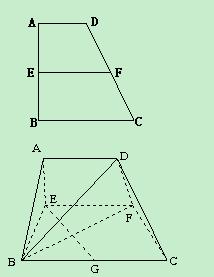
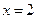 时,求证:
时,求证: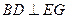 ;
; 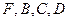 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为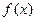 ,求
,求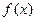 的最大值;
的最大值;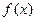 取得最大值时,求钝二面角
取得最大值时,求钝二面角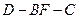 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.
,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点. D所成角的正弦值;
D所成角的正弦值; 的体积为
的体积为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
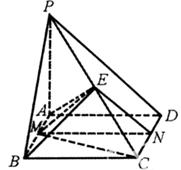
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
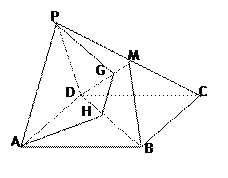
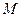 是棱
是棱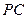 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: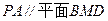 ;
;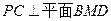 ;
;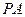 与直线
与直线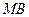 所成角的余弦值.
所成角的余弦值.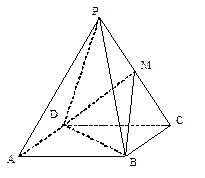
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, ,
, ,且
,且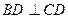 ,正方形
,正方形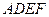 所在平面和平面
所在平面和平面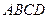 垂直,
垂直,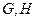 分别是
分别是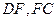 的中点.
的中点.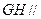 平面
平面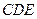 ;
;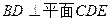 ;
; 的体积.
的体积.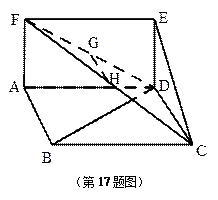
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 内及其边界上运动,并且总是保持PE
内及其边界上运动,并且总是保持PE AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是( ).
AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是( ).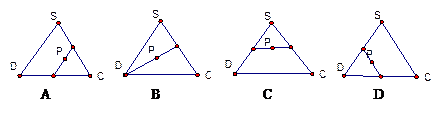
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com