【题目】下列四个命题：①任意两条直线都可以确定一个平面；②若两个平面有3个不同的公共点，则这两个平面重合；③直线a，b，c，若a与b共面，b与c共面，则a与c共面；④若直线l上有一点在平面α外，则l在平面α外.其中错误命题的个数是（ ）
A.1B.2C.3D.4
【答案】C
【解析】
两条异面直线不能确定一个平面；若两个平面有3个共线的公共点，则这两个平面相交；若a与b共面，b与c共面，则a与c不一定共面；若直线l上有一点在平面α外，则由直线与平面的位置关系得l在平面α外.
在①中，两条异面直线不能确定一个平面，故①错误；
在②中，若两个平面有3个不共线的公共点，则这两个平面重合，
若两个平面有3个共线的公共点，则这两个平面相交，故②错误；
在③中，直线a，b，c，若a与b共面，b与c共面，则a与c不一定共面，
如四面体S﹣ABC中，SA与AB共面，AB与BC共面，但SA与BC异面，故③错误；
在④中，若直线l上有一点在平面α外，则由直线与平面的位置关系得l在平面α外，故④正确.
故选：C
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案科目：高中数学 来源： 题型：
【题目】下列命题中正确的是（ ）
A.
是空间中的四点，若
不能构成空间基底，则共面
B.已知
为空间的一个基底，若
，则
也是空间的基底
C.若直线
的方向向量为
，平面
的法向量为
，则直线
D.若直线的方向向量为，平面的法向量为
，则直线与平面所成角的正弦值为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“科技引领，布局未来”科技研发是企业发展的驱动力量。
年，某企业连续
年累计研发投入搭
亿元，我们将研发投入与经营投入的比值记为研发投入占营收比，这年间的研发投入（单位：十亿元）用右图中的折现图表示，根据折线图和条形图，下列结论错误的使（ ）
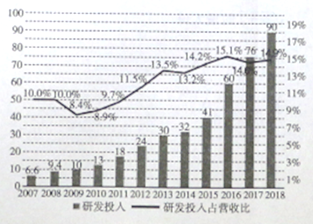
A. 
年至
年研发投入占营收比增量相比
年至
年增量大
B. 年至
年研发投入增量相比
年至
年增量小
C. 该企业连续年研发投入逐年增加
D. 该企业来连续年来研发投入占营收比逐年增加
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，椭圆
离心率为
，
、
是椭圆C的短轴端点，且到焦点的距离为
，点M在椭圆C上运动，且点M不与、重合，点N满足
．
（1）求椭圆C的方程；
（2）求四边形
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥P-ABC中，三条侧棱PA、PB、PC两两垂直，且
，
，又M是底面ABC内一点，则M到三个侧面的距离的平方和的最小值是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，满足acosB+bcosA=2ccosC．
（1）求角C的大小；
（2）若△ABC的周长为3，求△ABC的内切圆面积S的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次“综艺类和体育类节目，哪一类节目受中学生欢迎”的调查中，随机调查了男女各100名学生，其中女同学中有73人更爱看综艺类节目，另外27人更爱看体育类节目；男同学中有42人更爱看综艺类节目，另外58人更爱看体育类节目．
（1）根据以上数据填写如下
列联表：
综艺类 | 体育类 | 总计 | |
女 | |||
男 | |||
总计 |
（2）试判断是否有
的把握认为“中学生更爱看综艺类节目还是体育类节目与性别有关”．
参考公式：
，其中
.
临界值表：
| 0.025 | 0.01 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某水产品经销商销售某种鲜鱼，售价为每千克
元，成本为每千克
元，销售宗旨是当天进货当天销售，如果当天卖不完，那么未售出的部分全部处理，平均每千克损失
元.根据以往的市场调查，将市场日需求量（单位：千克）按
，
，
，
，
进行分组，得到如图的频率分布直方图.
（Ⅰ）未来连续三天内，连续两天该种鲜钱的日需求量不低于
千克，而另一天的日需求量低于千克的概率；
（Ⅱ）在频率分布直方图的日需求量分组中，以各组区间的中点值代表该组的各个值，并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率.若经销商每日进货
千克，记经销商每日利润为
（单位：元），求的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
