
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,B是钝角,且 ![]() a=2bsinA.
a=2bsinA.
(1)求B的大小;
(2)若△ABC的面积为 ![]() ,且b=7,求a+c的值;
,且b=7,求a+c的值;
(3)若b=6,求△ABC面积的最大值.
【答案】
(1)解:∵ ![]() ,
,
∴利用正弦定理可得: ![]() ,又sinA≠0,
,又sinA≠0,
∴可得: ![]() ,
,
∵B是钝角,
∴ ![]()
(2)解:∵ ![]() .
.
∴可得:ac=15,
∵b2=a2+c2﹣2accosB,
∴49=(a+c)2﹣ac,
∴a+c=8.
(3)解:∵b2=a2+c2﹣2accosB,
∴36=a2+c2+ac≥2ac+ac,
∴ac≤12,
∴ ![]() ,(当且仅当
,(当且仅当 ![]() 时面积取最大值
时面积取最大值 ![]() )
)
【解析】(1)利用正弦定理可得 ![]() ,结合sinA≠0,可求sinB,结合B是钝角,即可得解B的值.(2)由已知利用三角形面积公式可求ac=15,利用余弦定理即可得解a+c=8.(3)由余弦定理,基本不等式可得36=a2+c2+ac≥2ac+ac,解得ac≤12,利用三角形面积公式即可得解.
,结合sinA≠0,可求sinB,结合B是钝角,即可得解B的值.(2)由已知利用三角形面积公式可求ac=15,利用余弦定理即可得解a+c=8.(3)由余弦定理,基本不等式可得36=a2+c2+ac≥2ac+ac,解得ac≤12,利用三角形面积公式即可得解.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,若其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为 ![]() ,则圆的方程为( )
,则圆的方程为( )
A.(x+2)2+(y+3)2=9
B.(x+3)2+(y+5)2=25
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是双曲线 ![]() 的左右焦点,A为双曲线的右顶点,线段AF2的垂直平分线交双曲线与P,且|PF1|=3|PF2|,则该双曲线的离心率是( )
的左右焦点,A为双曲线的右顶点,线段AF2的垂直平分线交双曲线与P,且|PF1|=3|PF2|,则该双曲线的离心率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)是二次函数,如图是f′(x)的大致图象,若f(x)的极大值与极小值的和等于 ![]() ,则f(0)的值为( )
,则f(0)的值为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间[2,4]的有8人.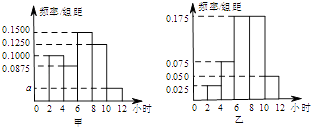
(1)求直方图中a的值及甲班学生每天平均学习时间在区间(10,12]的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中其中真命题个数是( )
①为了了解800名学生的成绩,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40;
②线性回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ;
;
③随机变量ξ服从正态分布N(2,σ2)(σ>0),若在(﹣∞,1)内取值的概率为0.1,则在(2,3)内的概率为0.4;
④若事件![]() 和
和![]() 满足关系
满足关系![]() ,则事件
,则事件![]() 和
和![]() 互斥.
互斥.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 分别是椭圆的左、右顶点,若过点
分别是椭圆的左、右顶点,若过点![]() 的直线与椭圆相交于不同两点
的直线与椭圆相交于不同两点![]() .
.
①求证:![]() ;
;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“数列{an}成等比数列”是“数列{lgan+1}成等差数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com