
已知函数 ,且
,且 ,函数
,函数 的图象经过点
的图象经过点 ,且
,且 与
与 的图象关于直线
的图象关于直线 对称,将函数
对称,将函数 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数 的图象.
的图象.
(Ⅰ)求函数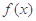 的解析式;
的解析式;
(Ⅱ)若 在区间
在区间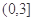 上的值不小于8,求实数
上的值不小于8,求实数 的取值范围.
的取值范围.
(III)若函数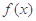 满足:对任意的
满足:对任意的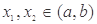 (其中
(其中 ),有
),有 ,称函数
,称函数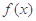 在
在 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数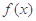 图象在
图象在 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
.(Ⅰ) (Ⅱ)a≥12(III)是
(Ⅱ)a≥12(III)是
【解析】本试题主要考查了函数的解析式和函数的单调性和函数的下凸形的运用。
(1)由题意得h(x)的图象经过(3,4),
代入得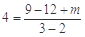 ,解得m=7. ∴
,解得m=7. ∴ 分
分
∴ .
.
(2)∵ ,
,
∴ 由已知有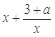 ≥8有a≥-x2+8x-3,
令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.∴ t(x)max=12.∴ a≥12
≥8有a≥-x2+8x-3,
令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.∴ t(x)max=12.∴ a≥12
(3) 的图象在
的图象在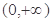 是“下凸的”,根据新定义证明,
是“下凸的”,根据新定义证明,
解:(Ⅰ)由题意得h(x)的图象经过(3,4),
代入得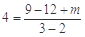 ,解得m=7.
1分
,解得m=7.
1分
∴ 2分
2分
∴ .
4分
.
4分
(Ⅱ)∵ ,
,
∴ 由已知有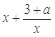 ≥8有a≥-x2+8x-3,
6分
≥8有a≥-x2+8x-3,
6分
令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.
∴ t(x)max=12.
∴ a≥12. 8分
(III) 的图象在
的图象在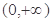 是“下凸的”.
9分
是“下凸的”.
9分


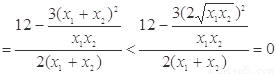

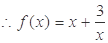 的图象在
的图象在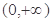 是“下凸的”.
12分
是“下凸的”.
12分


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| ||
| cosx+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() (
(![]() ),且
),且![]() .
.
(Ⅰ)试用含有![]() 的式子表示
的式子表示![]() ,并求
,并求![]() 的极值;
的极值;
(Ⅱ)对于函数![]() 图象上的不同两点
图象上的不同两点![]() ,
,![]() ,如果在函数图象上存在点
,如果在函数图象上存在点![]() (其中
(其中![]() ),使得点
),使得点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当![]() 时,又称
时,又称![]() 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数![]() 的图象上是否存在两点
的图象上是否存在两点![]() 、
、![]() 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出![]() 、
、![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省上高二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
 ,且给定条件p:
,且给定条件p: .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省长沙市高三第三次月考文科数学卷 题型:解答题
已知函数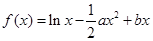 (
( ),且
),且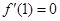 .
.
(Ⅰ)试用含有 的式子表示
的式子表示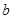 ,并求
,并求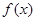 的极值;
的极值;
(Ⅱ)对于函数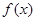 图象上的不同两点
图象上的不同两点 ,
,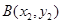 ,如果在函数图象上
,如果在函数图象上 存在点
存在点 (其中
(其中 ),使得点
),使得点 处的切线
处的切线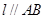 ,则称
,则称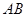 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当 时,又称
时,又称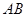 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数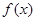 的图象上是否存在两点
的图象上是否存在两点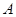 、
、 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出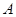 、
、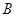 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com