
【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=![]() , SB=
, SB=![]() .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC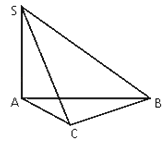
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
已知椭圆![]() 的短轴长为
的短轴长为![]() ,且与抛物线
,且与抛物线![]() 有共同的焦点,椭圆
有共同的焦点,椭圆![]() 的左顶点为A,右顶点为
的左顶点为A,右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.
两点.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)求线段![]() 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段![]() 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
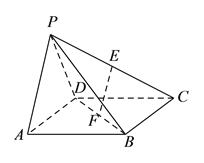
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.
(![]() )证明:
)证明: ![]() 平面
平面![]() .
.
(![]() )证明:平面
)证明:平面![]() 平面
平面![]() .
.
(![]() )当
)当![]() 上的动点
上的动点![]() 满足什么条件时,使三棱锥
满足什么条件时,使三棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 体积的比值为
体积的比值为![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC,平面PAB与平面PAD的位置关系是( )
A.平面PAB与平面PAD,PBC垂直
B.它们都分别相交且互相垂直
C.平面PAB与平面PAD垂直,与平面PBC相交但不垂直
D.平面PAB与平面PBC垂直,与平面PAD相交但不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中, ![]() ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
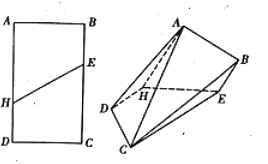
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央电视台为了解该卫视《朗读者》节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
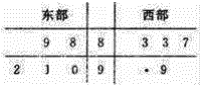
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获益匪浅,现从观看节目的观众中随机统计了![]() 位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
年龄 |
|
|
|
|
周均学习成语知识时间 |
|
|
|
|
由表中数据,试求线性回归方程![]() ,并预测年龄为
,并预测年龄为![]() 岁观众周均学习阅读经典知识的时间.
岁观众周均学习阅读经典知识的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】毕节市正实施“五城同创”计划。为搞好卫生维护工作,政府招聘了200名市民志愿者,按年龄情况进行统计的频率分布表和频率分布直方图如下:
分组(岁) | 频数 | 频率 |
[30,35) | 20 | 0.1 |
[35,40) | 20 | 0.1 |
[40,45) | ① | 0.2 |
[45,50) | ② | ③ |
[50,55] | 40 | 0.2 |
合计 | 200 | 1 |
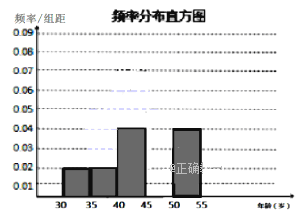
(1)频率分布表中的①②③位置应填什么数?补全频率分布直方图;
(2)根据频率分布直方图估计这200名志愿者的平均年龄.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com