
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数),
为参数),![]() 为曲线
为曲线![]() 上的动点,动点
上的动点,动点![]() 满足
满足![]() (
(![]() 且
且![]() ),
),![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)在以坐标原点为极点,以![]() 轴的正半轴为极轴的极坐标系中,
轴的正半轴为极轴的极坐标系中, ![]() 点的极坐标为
点的极坐标为![]() ,射线
,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,已知
,已知![]() 面积的最大值为
面积的最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)2
【解析】分析:(1)设![]() ,
, ![]() ,根据
,根据![]() ,推出
,推出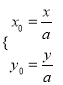 ,代入到
,代入到![]() ,消去参数即可求得曲线
,消去参数即可求得曲线![]() 的方程及其表示的轨迹;(2)法1:先求出
的方程及其表示的轨迹;(2)法1:先求出![]() 点的直角坐标,再求出直线
点的直角坐标,再求出直线![]() 的普通方程,再根据题设条件设
的普通方程,再根据题设条件设![]() 点坐标为
点坐标为![]() ,然后根据两点之间距离公式及三角函数的图象与性质,结合
,然后根据两点之间距离公式及三角函数的图象与性质,结合![]() 面积的最大值为
面积的最大值为![]() ,即可求得
,即可求得![]() 的值;法2:将
的值;法2:将![]() ,
, ![]() 代入
代入![]() ,即可求得
,即可求得![]() ,再根据三角形面积公式及三角函数的图象与性质,结合
,再根据三角形面积公式及三角函数的图象与性质,结合![]() 面积的最大值为
面积的最大值为![]() ,即可求得
,即可求得![]() 的值.
的值.
详解:(1)设![]() ,
, ![]() ,由
,由![]() 得
得![]() .
.
∴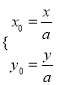
∵![]() 在
在![]() 上
上
∴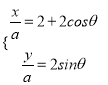 即
即![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() 得
得![]() .
.
∴曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(2)法1: ![]() 点的直角坐标为
点的直角坐标为![]() .
.
∴直线![]() 的普通方程为
的普通方程为![]() ,即
,即![]() .
.
设![]() 点坐标为
点坐标为![]() ,则
,则![]() 点到直线
点到直线![]() 的距离
的距离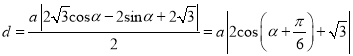 .
.
∴当![]() 时,
时, ![]()
∴![]() 的最大值为
的最大值为![]()
∴![]() .
.
法2:将![]() ,
, ![]() 代入
代入![]() 并整理得:
并整理得: ![]() ,令
,令![]() 得
得![]() .
.
∴![]()
∴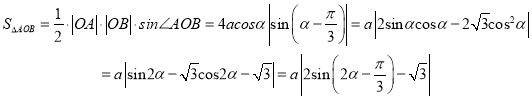
∴当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,依题意
,依题意![]() ,∴
,∴![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险的基准保费为
座以下私家车投保交强险的基准保费为![]() 元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况想联系,最终保费
元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况想联系,最终保费![]() 基准保费
基准保费![]() (
(![]() 与道路交通事故相联系的浮动比率),具体情况如下表:
与道路交通事故相联系的浮动比率),具体情况如下表:

为了解某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
若以这![]() 辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列四个命题中,其中真命题是( )
①“若![]() ,则
,则![]() ”的逆命题;
”的逆命题;
②“若![]() ,则
,则![]() ”的否命题;
”的否命题;
③“若![]() ,则方程
,则方程![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“等边三角形的三个内角均为![]() ”的逆命题.
”的逆命题.
A. ①② B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地新建一家服装厂,从今年7月份开始投产,并且前4个月的产量分别为![]() 万件、
万件、![]() 万件、
万件、![]() 万件、
万件、![]() 万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:
万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:![]() ,
,![]() ,
,![]() ,
,![]() .你将利用零一种模型去估算以后几个月的产量?
.你将利用零一种模型去估算以后几个月的产量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系![]() 自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
(2)某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0.01%,若初始时含杂质0.2%,每次过滤可使杂质含量减少三分之一,问至少应过滤几次才能使得这种液体达到要求?(已知![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com