
A、若ab>0,则
| ||||
B、函数y=cosx+
| ||||
| C、函数y=2x+2-x的最小值为2 | ||||
D、若x∈(0,1),则函数y=lnx+
|
| a |
| b |
| b |
| a |
| π |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 1 |
| -t |
| a |
| b |
| b |
| a |
| b |
| a |
| a |
| b |
|
| π |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 1 |
| t |
| 1 |
| -t |
-t•
|


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
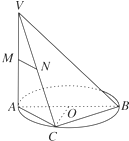 如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )
如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )| A、平面VAC⊥平面VBC |
| B、OC⊥平面VAC |
| C、MN与BC所成的角为45° |
| D、MN∥AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、x-y+1=0 |
| B、x+y+1=0 |
| C、x-y-1=0 |
| D、x+y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | |
| 降雨量x(毫米) | 1500 | 1400 | 1900 | 1600 | 2100 |
| 发电量y(亿千瓦时) | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
| ? |
| y |
| ? |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B=|x|log2(x+2)<4}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B=|x|log2(x+2)<4}.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 8 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、必要而不充分条件 |
| B、充要条件 |
| C、充分而不必要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com