
【题目】已知函数f(x)=4sinxcos(x+ ![]() )+m(x∈R,m为常数),其最大值为2. (Ⅰ)求实数m的值;
)+m(x∈R,m为常数),其最大值为2. (Ⅰ)求实数m的值;
(Ⅱ)若f(α)=﹣ ![]() (﹣
(﹣ ![]() <α<0),求cos2α的值.
<α<0),求cos2α的值.
【答案】解:(Ⅰ)函数f(x)=4sinxcos(x+ ![]() )+m(x∈R,m为常数),
)+m(x∈R,m为常数),
化简可得:f(x)=4sinxcosxcos ![]() ﹣4sin2xsin
﹣4sin2xsin ![]() +m=sin2x﹣2
+m=sin2x﹣2 ![]() sin2x+m
sin2x+m
=sin2x+ ![]() cos2x﹣
cos2x﹣ ![]() +m=2sin(2x+
+m=2sin(2x+ ![]() )﹣
)﹣ ![]() +m
+m
∵最大值为2.
即2﹣ ![]() +m=2,
+m=2,
可得m= ![]() .
.
(Ⅱ)由f(α)=﹣ ![]() (﹣
(﹣ ![]() <α<0),即2sin(2α+
<α<0),即2sin(2α+ ![]() )=
)= ![]() .
.
∴sin(2α+ ![]() )=
)= ![]()
∵﹣ ![]() <α<0
<α<0
∴ ![]() <2α+
<2α+ ![]() <
< ![]() .
.
∴cos(2α+ ![]() )=
)= ![]() ;
;
那么cos2α=cos[(2α ![]() )
) ![]() ]=cos(2α+
]=cos(2α+ ![]() )cos
)cos ![]() +sin(2α+
+sin(2α+ ![]() )sin
)sin ![]() =
= ![]()
【解析】(Ⅰ)利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,求出最大值,令其等于2,可得实数m的值.(Ⅱ)f(α)=﹣ ![]() (﹣
(﹣ ![]() <α<0)带入计算,找出等式关系,利用二倍角公式求解即可.
<α<0)带入计算,找出等式关系,利用二倍角公式求解即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则2(x4﹣x1)+(x3﹣x2)的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三个内角A,B,C依次成等差数列,若sin2B=sinAsinC,则△ABC形状是( )
A.锐角三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且 ![]() ,
, ![]() .
. 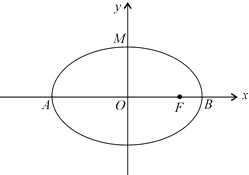
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为M,直线l交椭圆于P,Q两点,问:是否存在直线l,使点F恰为△PQM的垂心?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x20的均值和方差分别为1和8,若yi=2xi+3(i=1,2,…,20),则y1 , y2 , …,y20的均值和方差分别是( )
A.5,32
B.5,19
C.1,32
D.4,35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,f(x)=aln(x﹣1)+x,f′(2)=2
(1)求a的值,并求曲线y=f(x)在点(2,f(2))处的切线方程y=g(x);
(2)设h(x)=mf′(x)+g(x)+1,若对任意的x∈[2,4],h(x)>0,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com