
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料![]() ,乙材料
,乙材料![]() .用5个工时;生产一件产品B需要甲材料
.用5个工时;生产一件产品B需要甲材料![]() ,乙材料
,乙材料![]()
![]() ,用3个工时。生产一件产品A的利润为2100元,生产一件产品B的利润为900元,该企业现有甲材料150
,用3个工时。生产一件产品A的利润为2100元,生产一件产品B的利润为900元,该企业现有甲材料150![]() ,乙材料
,乙材料![]() ,则在不超过600个工时的条件下,生产产品A,产品B的利润之和的最大值为______________元.
,则在不超过600个工时的条件下,生产产品A,产品B的利润之和的最大值为______________元.
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若满足条件:存在
,若满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则称
,则称![]() 为“倍缩函数”.若函数
为“倍缩函数”.若函数![]() 为“倍缩函数”,则实数
为“倍缩函数”,则实数![]() 的取值范围是
的取值范围是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求直线
时,求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() ,证明:
,证明:![]() 是与
是与![]() 无关的定值.
无关的定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
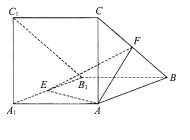
【题目】【2018届北京市海淀区】如图,三棱柱![]() 侧面
侧面![]() 底面
底面![]() ,
, ![]()
![]()
![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求三棱柱![]() 的体积;
的体积;
(Ⅲ)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
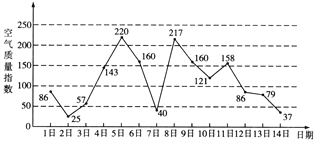
(Ⅰ)求3月1日到14日空气质量指数的中位数;
(Ⅱ)求此人到达当日空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为100的调查样本,其中城镇户籍与农民户籍各50人;男性60人,女性40人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
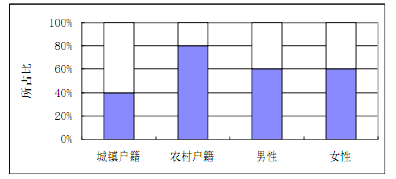
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别无关
C. 倾向选择生育二胎的人员中,男性人数与女性人数相同
D. 倾向选择生育二的人员中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com