

图1-2-18
思路分析:要证明EF∥BC,想通过角之间的关系达到目的显然是不可能的,而要利用成比例线段判定两直线平行的判定定理,图中又没有平行条件,因此要设法作出平行线,以便利用判定定理.作平行线时,要充分考虑到中点D条件的应用.



(1) (2) (3)
分析一:延长AD至G,使DG=MD,连结BG、CG,如图(1),则四边形BGCM为平行四边形,可以立即将![]() 转化成中间比
转化成中间比![]() .
.
解法一:延长AD至G,使DG=MD,连结BG、CG.
∵BD=DC,MD=DG,
∴四边形BGCM为平行四边形.
∴EC∥BG,FB∥CG.
∴![]() =
=![]() ,
,![]() =
=![]() .
.
∴![]() =
=![]() .∴EF∥BC.
.∴EF∥BC.
分析二:过A作BC的平行线,与BF、CE的延长线分别交于G、H,如图(2),则
![]() .要证明
.要证明![]() ,只要证AH=AG,这是不难解决的.
,只要证AH=AG,这是不难解决的.
解法二:过A作BC的平行线,与BF、CE的延长线分别交于G、H.
∵AH∥DC,AG∥BD,
∴![]() ∵BD=DC,∴AH=AG.
∵BD=DC,∴AH=AG.
∵HG∥BC,∴![]() .
.
∵AH=AG,∴![]() .∴EF∥BC.
.∴EF∥BC.
分析三:如图(3),过M作BC的平行线,分别与AB、AC交于G、H,
∵BD=DC,GM=MH.要证EF∥BC,只要证![]() ,这可以通过中间比立即证得.
,这可以通过中间比立即证得.
解法三:过M作BC的平行线,分别与AB、AC交于G、H,
则![]() .
.
∵BD=DC,∴GM=MH.
∵GH∥BC,![]() ∵GM=MH,∴
∵GM=MH,∴![]() ∴EF∥BC.
∴EF∥BC.


科目:高中数学 来源: 题型:044
(1)![]() +
+![]() =
=![]() 还成立吗?如果成立,请给出证明;如果不成立,请说明理由.?
还成立吗?如果成立,请给出证明;如果不成立,请说明理由.?
(2)请找出S△ABD、S△BED和S△BDC间的关系式,并给出证明.?

图1-2-18
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)![]() +
+![]() =
=![]() 还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
(2)请找出S△ABD、S△BED和S△BDC间的关系式,并给出证明.
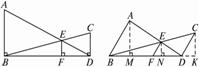
图1-2-18
查看答案和解析>>
科目:高中数学 来源: 题型:
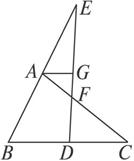
图
(1)求证:FG![]() ED=FD
ED=FD![]() EG;
EG;
(2)如图![]() ED=FD
ED=FD![]() EG还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
EG还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
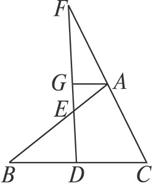
图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com