
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
【答案】(1)C1:(x+4)2+(y﹣3)2=1;C2:![]() ,(2)点Q(
,(2)点Q(![]() ,﹣
,﹣![]() )
)
【解析】试题分析:(1)分别消去两曲线参数方程中的参数得到两曲线的直角坐标方程,即可得到曲线![]() 表示一个圆;曲线
表示一个圆;曲线![]() 表示一个椭圆;(2)把
表示一个椭圆;(2)把![]() 的值代入曲线
的值代入曲线![]() 的参数方程得点
的参数方程得点![]() 的坐标,然后把直线的参数方程化为普通方程,根据曲线
的坐标,然后把直线的参数方程化为普通方程,根据曲线![]() 的参数方程设出
的参数方程设出![]() 的坐标,利用中点坐标公式表示出
的坐标,利用中点坐标公式表示出![]() 的坐标,利用点到直线的距离公式标准处
的坐标,利用点到直线的距离公式标准处![]() 到已知直线的距离,利用两角差的正弦函数公式化简后,利用正弦函数的值域即可得到距离的最小值.
到已知直线的距离,利用两角差的正弦函数公式化简后,利用正弦函数的值域即可得到距离的最小值.
试题解析:(1)![]()
![]() 为圆心是
为圆心是![]() ,半径是1的圆,
,半径是1的圆, ![]() 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在![]() 轴,长半轴长是8,短半轴长是3的椭圆.
轴,长半轴长是8,短半轴长是3的椭圆.
(2)当![]() 时,
时, ![]() ,故
,故![]()
![]() 的普通方程为
的普通方程为![]() ,
, ![]() 到
到![]() 的距离
的距离![]()
所以当![]() 时,
时, ![]() 取得最小值
取得最小值![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( ) 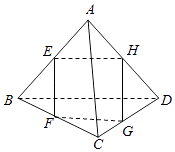
A.2对
B.4对
C.6对
D.8对
查看答案和解析>>
科目:高中数学 来源: 题型:
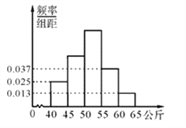
【题目】人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
(Ⅰ)求该校抽取的学生总数以及第2组的频率;
(Ⅱ)学校为进一步了解学生的身体素质,在第1组、第2组、第3组中用分层抽样的方法抽取6人进行测试.若从这6人中随机选取2人去共同完成某项任务,求这2人来自于同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布![]() ,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:

(注:表中试卷编号![]() )
)
(1)列出表中试卷得分为126分的试卷编号(写出具体数据);
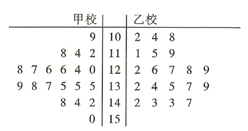
(2)该市又从乙校中也用系统抽样的方法抽取了20份试卷,将甲乙两校这40份试卷的得分制作了茎叶图(如图6),试通过茎叶图比较两校学生成绩的平均分及分散程度(均不要求计算出具体值,给出结论即可);
(3)在第(2)问的前提下,从甲乙两校这40名学生中,从成绩在140分以上(含140分)的学生中任意抽取3人,该3人在全市前15名的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
(附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式a|x|>x2﹣ ![]() 对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
A.( ![]() ,1)∪(1,+∞)
,1)∪(1,+∞)
B.(0, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.( ![]() ,1)∪(1,2)
,1)∪(1,2)
D.(0, ![]() )∪(1,2)
)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
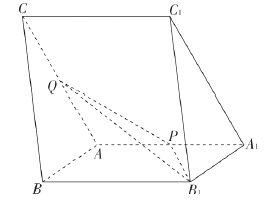
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x+y﹣8=0与直线x﹣2y+1=0交于点P.
(1)求过点P且平行于直线4x﹣3y﹣7=0的直线11的方程;(结果都写成一般方程形式)
(2)求过点P的所有直线中使原点O到此直线的距离最大的直线12的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com