
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史。某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位; ![]() )数据,将数据分组如下表:
)数据,将数据分组如下表:
分组 | 频数 | 频率 |
| 4 | |
| 26 | |
| ||
| 28 | |
| 10 | |
| 2 | |
合计 | 100 |
(1)在答题卡上完成频率分布表;
(2)以表中的频率作为概率,估计重量落在![]() 中的概率及重量小于2.45的概率是多少?
中的概率及重量小于2.45的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)具有较强的相关性,且两者之间有如下对应数据:
(单位:万元)具有较强的相关性,且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中的线性回归方程,当广告费支出为10万元时,预测销售额是多少?
参考数据: ![]() ,
,![]() ,
,![]() 。
。
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为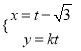 (
(![]() 为参数),直线
为参数),直线![]() 的参数程为
的参数程为 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 的动点,求点
的动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两人约定在20∶00到21∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20∶00至21∶00各时刻相见的可能性是相等的,则他们两人在约定时间内相见的概率为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com