
【题目】A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
A组:10,11,12,13,14,15,16
B组:12,13,15,16,17,14,a
假设所有病人的康复时间互相独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果人康复时间的方差相等?(结论不要求证明)
【答案】(I)![]() ,(II)
,(II)![]() ,(III)
,(III)![]() 或18
或18
【解析】
针对甲有7种情况,康复时间不少于14天有3种情况,概率为![]() ;如果
;如果![]() ,甲、乙随机各取一人有49种情况,用列举法列出甲的康复时间比乙的康复时间长的情况有10种,概率为
,甲、乙随机各取一人有49种情况,用列举法列出甲的康复时间比乙的康复时间长的情况有10种,概率为![]() ,由于A组数据为10,11,12,13,14,15,16;B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,由于A,B两组病人康复时间的方差相等,即波动相同,所以
,由于A组数据为10,11,12,13,14,15,16;B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,由于A,B两组病人康复时间的方差相等,即波动相同,所以![]() 或18.
或18.
(1)甲有7种取法,康复时间不少于14天的有3种取法,所以概率![]() ;
;
(2)如果![]() ,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙共有49种取法,甲的康复时间比乙的康复时间长的列举如下:(13,12),(14,12),(14,13),(15,12),(15,13),(15,14),(16,12)(16,13),(16,15),(16,14)有10种取法,所以概率P=
,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙共有49种取法,甲的康复时间比乙的康复时间长的列举如下:(13,12),(14,12),(14,13),(15,12),(15,13),(15,14),(16,12)(16,13),(16,15),(16,14)有10种取法,所以概率P=![]()
(3)把B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,可见当a=11或a=18时,与A组数据方差相等。
【考点精析】认真审题,首先需要了解极差、方差与标准差(标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(2015·湖北)设函数![]() ,
,![]() 的定义域均为
的定义域均为![]() ,且
,且![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求![]() ,
,![]() 的解析式,并证明:当
的解析式,并证明:当![]() 时,
时,![]() ,
,![]() ;
;
(Ⅱ)设![]() ,
,![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设fn(x)是等比数列1,x,x2...,xn的各项和,其中x>0,n![]() N, ,n≥2,
N, ,n≥2,
(1)证明:函数Fn(x)=fn(x)-2在(![]() ,1)内有且仅有一个零点(记为xn),且xn=
,1)内有且仅有一个零点(记为xn),且xn=![]() +
+![]() xnn+1;
xnn+1;
(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)与gn(x)的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=![]() )
)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
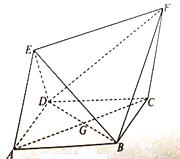
【题目】如图,四边形 ![]() 为菱形,四边形
为菱形,四边形 ![]() 为平行四边形,设
为平行四边形,设 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,
, ![]() .
.
(1)证明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() 与平面
与平面 ![]() 所成角为60°,求二面角
所成角为60°,求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为4π,则( )
的最小正周期为4π,则( )
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于直线 ![]() 对称
对称
C.函数f(x)图象上的所有点向右平移 ![]() 个单位长度后,所得的图象关于原点对称
个单位长度后,所得的图象关于原点对称
D.函数f(x)在区间(0,π)上单调递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com