
【题目】设函数f(x)=ex-ax-1.
(1)当a>0时,设函数f(x)的最小值为g(a),求证:g(a)≤0;
(2)求证:对任意的正整数n,都有1n+1+2n+1+3n+1+…+nn+1<(n+1)n+1.
【答案】(1)见解析(2)见解析.
【解析】试题分析:(1)在a>0的情况下讨论函数的单调性,求出函数的小值g(a)=a-alna-1,再对这个函数求导,研究这个函数的最大值g(1)=0,故g(a)≤0。(2)结合第一问得到x>0时,总有ex>x+1,两边变形得到(x+1)n+1<(ex)n+1=e(n+1)x.再利用赋值法得到结果即可。
解析:
(1)由a>0及f′(x)=ex-a可得,函数f(x)在(-∞,lna)上单调递减,
在(lna,+∞)上单调递增,
故函数f(x)的最小值为g(a)=f(lna)=elna-alna-1=a-alna-1,则g′(a)=-lna,
故当a∈(0,1)时,g′(a)>0;
当a∈(1,+∞)时,g′(a)<0,
从而可知g(a)在(0,1)上单调递增,
在(1,+∞)上单调递减,且g(1)=0,故g(a)≤0.
(2)由(1)可知,当a=1时,总有f(x)=ex-x-1≥0,
当且仅当x=0时等号成立,即当x>0时,总有ex>x+1.
于是,可得(x+1)n+1<(ex)n+1=e(n+1)x.
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() n+1<e-n;
n+1<e-n;
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() n+1<e-(n-1);
n+1<e-(n-1);
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() n+1<e-(n-2);
n+1<e-(n-2);
…
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() n+1<e-1.
n+1<e-1.
对以上各式求和可得:
![]() n+1+
n+1+![]() n+1+
n+1+![]() n+1+…+
n+1+…+![]() n+1<e-n+e-(n-1)+e-(n-2)+…+e-1
n+1<e-n+e-(n-1)+e-(n-2)+…+e-1
=![]() =
=![]() =
=![]() <
<![]() <1.
<1.
故对任意的正整数n,都有1n+1+2n+1+3n+1+…+nn+1<(n+1)n+1.


科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() 的重心恰好在圆
的重心恰好在圆![]() 上,求
上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
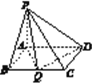
【题目】在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=![]() BC(a>0).
BC(a>0).
(1)当a=1时,求证:BD⊥PC;
(2)若BC边上有且只有一个点Q,使得PQ⊥QD,求此时二面角A-PD-Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)=-f(x)且f(x)在[-1,0]上是增函数,给出下列四个命题:
①f(x)是周期函数;②f(x)的图象关于x=1对称;③f(x)在[1,2]上是减函数;④f(2)=f(0).
其中正确命题的序号是____________.(请把正确命题的序号全部写出来)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(ln x-ax)有两个极值点,则实数a的取值范围是( )
A. (-∞,0) B. ![]()
C. (0,1) D. (0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图与侧视图是腰长为6的等腰直角三角形,俯视图是正方形.
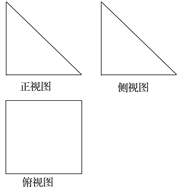
(1)请画出该几何体的直观图,并求出它的体积;
(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1?如何组拼?试证明你的结论;
(3)在(2)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1-![]() )是R上的偶函数.
)是R上的偶函数.
(1)对任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求实数m的取值范围.
≥2x+1恒成立,求实数m的取值范围.
(2)令g(x)=1-![]() ,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com