练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知$\overrightarrow a$，$\overrightarrow b$是单位向量，$\overrightarrow a•\overrightarrow b=0$，且向量$\overrightarrow c$满足$|\overrightarrow c-\overrightarrow a-\overrightarrow b|$=1，则|$\overrightarrow c$|的取值范围是（　　）
    A．$[\sqrt{2}-1，\;\sqrt{2}+1]$B．$[\sqrt{2}-1，\;\sqrt{2}]$C．$[\sqrt{2}，\;\sqrt{2}+1]$D．$[2-\sqrt{2}，\;2+\sqrt{2}]$

    分析 由题意画出图形，$|\overrightarrow c-\overrightarrow a-\overrightarrow b|$=1的几何意义为在以原点为起点的情况下，$\overrightarrow{c}$的终点到$（\overrightarrow{a}+\overrightarrow{b}）$的终点的距离为1，由此求得|$\overrightarrow c$|的取值范围．

    解答 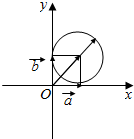解：如图，
    由$|\overrightarrow c-\overrightarrow a-\overrightarrow b|$=1，得$|\overrightarrow{c}-（\overrightarrow{a}+\overrightarrow{b}）|=1$，
    即在以原点为起点的情况下，$\overrightarrow{c}$的终点到$（\overrightarrow{a}+\overrightarrow{b}）$的终点的距离为1．
    ∴|$\overrightarrow c$|的取值范围是$[\sqrt{2}-1，\sqrt{2}+1]$．
    故选：A．

    点评 本题考查平面向量的数量积运算，考查了数形结合的解题思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．对于无穷数列{Tn}，若正整数n0，使得n≥n0（n∈N*）时，有Tn+1＞Tn，则称{Tn}为“n0～不减数列”．
    （1）设s，t为正整数，且s＞t，甲：{xn}为“s～不减数列”，乙：{xn}为“t～不减数列”．
    试判断命题：“甲是乙的充分条件”的真假，并说明理由；
    （2）已知函数y=f（x）与函数y=-$\frac{1}{x}$+2的图象关于直线y=x对称，数列{an}满足a1=3，an+1=f（an）（n∈N*），如果{an}为“n0～不减数列”，试求n0的最小值；
    （3）设yn=$\left\{\begin{array}{l}{f（\frac{4}{3}），（n=1）}\\{（\frac{1}{{2}^{n}}+1）cosnπ，（n≥2，n∈{N}^{*}）}\end{array}\right.$，且xn-λyn=2n，是否存在实数λ使得{xn}为“$\frac{1}{2}$f（f（$\frac{4}{3}$））～不减数列”？若存在，求出λ的取值范围，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设P1和P2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$上的两点，线段P1P2的中点为M，直线P1P2不经过坐标原点O．
    （1）若直线P1P2和直线OM的斜率都存在且分别为k1和k2，求证：k1k2=$\frac{b^2}{a^2}$；
    （2）若双曲线的焦点分别为${F_1}（-\sqrt{3}，0）$、${F_2}（\sqrt{3}，0）$，点P1的坐标为（2，1），直线OM的斜率为$\frac{3}{2}$，求由四点P1、F1、P2、F2所围成四边形P1F1P2F2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知{an}是等比数列，给出以下四个命题：①{2a3n-1}是等比数列；②{an+an+1}是等比数列；③{anan+1}是等比数列；④{lg|an|}是等比数列，下列命题中正确的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．对于数列{an}，称$P（{a_k}）=\frac{1}{k-1}（|{{a_1}-{a_2}}|+|{{a_2}-{a_3}}|+…+|{{a_{k-1}}-{a_k}}|）$（其中k≥2，k∈N）为数列{an}的前k项“波动均值”．若对任意的k≥2，k∈N，都有P（ak+1）＜P（ak），则称数列{an}为“趋稳数列”．
    （1）若数列1，x，2为“趋稳数列”，求x的取值范围；
    （2）若各项均为正数的等比数列{bn}的公比q∈（0，1），求证：{bn}是“趋稳数列”；
    （3）已知数列{an}的首项为1，各项均为整数，前k项的和为Sk．且对任意k≥2，k∈N，都有3P（Sk）=2P（ak），试计算：$C_n^2P（{a_2}）+2C_n^3P（{a_3}）+…+（n-1）C_n^nP（{a_n}）$（n≥2，n∈N）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

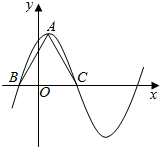    10．函数f（x）=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为等边三角形．将函数f（x）的图象上各点的横坐标变为原来的π倍，将所得图象向右平移$\frac{2π}{3}$个单位，再向上平移1个单位，得到函数y=g（x）的图象
    （1）求函数g（x）的解析式；
    （2）求h（x）=lg[g（x）-$\frac{5}{2}$]的定义域；
    （3）若3sin2$\frac{x}{2}$-$\sqrt{3}$m[g（x）-1]≥m+2对任意x∈[0，2π]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．$若log_a^{\;}\frac{2}{3}＜1，（a＞0且a≠1）$，则a的取值范围是（　　）
    A．（$\frac{2}{3}$，1）B．（0，$\frac{2}{3}$）∪（1，+∞）C．（1，+∞）D．（0，$\frac{2}{3}$）∪（$\frac{2}{3}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知⊙O1与⊙O1的半径分别为5cm和3cm，圆心距O1O1=7cm，则两圆的位置关系相交．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．对于数列{an}，称P（ak）=$\frac{1}{k-1}（|{{a_1}-{a_2}}|+|{{a_2}-{a_3}}|+…+|{{a_{k-1}}-{a_k}}|）$（其中k≥2，k∈N）为数列{an}的前k项“波动均值”．若对任意的k≥2，k∈N，都有P（ak+1）＜P（ak），则称数列{an}为“趋稳数列”．
    （1）若数列1，x，2为“趋稳数列”，求x的取值范围；
    （2）已知等差数列{an}的公差为d，且a1＞0，d＞0，其前n项和记为Sn，试计算：Cn2P（S2）+Cn3P（S3）+…+CnnP（Sn）（n≥2，n∈N）；
    （3）若各项均为正数的等比数列{bn}的公比q∈（0，1），求证：{bn}是“趋稳数列”．

    查看答案和解析>>

    同步练习册答案