
【题目】已知椭圆![]() 过点
过点![]() ,且椭圆的离心率
,且椭圆的离心率![]() .
.
(1)求椭圆的标淮方程;
(2)直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 、
、![]() 两点,椭圆的右顶点为
两点,椭圆的右顶点为![]() ,试判断
,试判断![]() 是否能为直角.若能为直角,求出直线
是否能为直角.若能为直角,求出直线![]() 的方程,若不行,请说明理由.
的方程,若不行,请说明理由.
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】某校要通过选拔赛选取一名同学参加市级乒乓球单打比赛,选拔赛采取淘汰制,败者直接出局。现有两种赛制方案:三局两胜制和五局三胜制。问两选手对决时,选择何种赛制更有利于选拔出实力最强的选手,并说明理由。(设各局胜负相互独立,各选手水平互不相同。)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一条准线方程为
,一条准线方程为![]()
⑴求椭圆![]() 的方程;
的方程;
⑵设![]() 为椭圆
为椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,且
为坐标原点,且![]() .
.
①当直线![]() 的倾斜角为
的倾斜角为![]() 时,求
时,求![]() 的面积;
的面积;
②是否存在以原点![]() 为圆心的定圆,使得该定圆始终与直线
为圆心的定圆,使得该定圆始终与直线![]() 相切?若存在,请求出该定圆方程;若不存在,请说明理由.
相切?若存在,请求出该定圆方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有如下三个命题:
甲:相交直线l、m都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内;
内;
乙:直线l、m中至少有一条与平面![]() 相交;
相交;
丙:平面![]() 与平面
与平面![]() 相交.
相交.
当甲成立时![]()
![]()
A. 乙是丙的充分而不必要条件
B. 乙是丙的必要而不充分条件
C. 乙是丙的充分且必要条件
D. 乙既不是丙的充分条件又不是丙的必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是棱
分别是棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点,点
的中点,点![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() 上移动,且
上移动,且![]() .
.
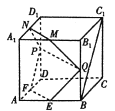
(1)当![]() 时,证明:直线
时,证明:直线![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使面
,使面![]() 与面
与面![]() 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,该椭圆经过点
,该椭圆经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 是圆
是圆![]() 上任意一点,由
上任意一点,由![]() 引椭圆
引椭圆![]() 的两条切线
的两条切线![]() ,
,![]() ,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
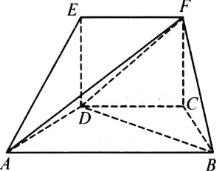
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com