
【题目】现有10个不同的产品,其中4个次品,6个正品.现每次取其中一个进行测试,直到4个次品全测完为止,若最后一个次品恰好在第五次测试时被发现,则该情况出现的概率是_______.
【答案】![]()
【解析】
先求出基本事件总数n![]() ,最后一个次品恰好在第五次测试时被发现包含的基本事件为:优先考虑第五次(位置)测试.这五次测试必有一次是测试正品,有C61种,4只次品必有一只排在第五次测试,有C41种,那么其余3只次品和一只正品将在第1至第4次测试中实现,有A44种.根据分步计数原理有C61C41A44种.由此能求出最后一个次品恰好在第五次测试时被发现的概率.
,最后一个次品恰好在第五次测试时被发现包含的基本事件为:优先考虑第五次(位置)测试.这五次测试必有一次是测试正品,有C61种,4只次品必有一只排在第五次测试,有C41种,那么其余3只次品和一只正品将在第1至第4次测试中实现,有A44种.根据分步计数原理有C61C41A44种.由此能求出最后一个次品恰好在第五次测试时被发现的概率.
现有10个不同的产品,其中4个次品,6个正品.现每次取其中一个进行测试,
直到4个次品全测完为止,最后一个次品恰好在第五次测试时被发现,
基本事件总数n![]() ,
,
最后一个次品恰好在第五次测试时被发现包含的基本事件为:
优先考虑第五次(位置)测试.这五次测试必有一次是测试正品,有C61种,
4只次品必有一只排在第五次测试,有C41种,
那么其余3只次品和一只正品将在第1至第4次测试中实现,有A44种.
于是根据分步计数原理有C61C41A44种.
∴最后一个次品恰好在第五次测试时被发现的概率p![]() .
.
故答案为:![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系.过点
轴建立直角坐标系.过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 关于直线
关于直线![]() 对称,且与曲线
对称,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下顶点、右顶点、右焦点分别为B2、B1、A、F,延长B1F与AB2交于点P,若∠B1PA为钝角,则此椭圆的离心率e的取值范围为_____.
的上、下顶点、右顶点、右焦点分别为B2、B1、A、F,延长B1F与AB2交于点P,若∠B1PA为钝角,则此椭圆的离心率e的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说,年过半百的笛卡尔担任瑞典一小公国的公主克里斯蒂娜的数学老师,日久生情,彼此爱慕,其父国王知情后大怒,将笛卡尔流放回法国,并软禁公主,笛卡尔回法国后染上黑死病,连连给公主写信,死前最后一封信只有一个公式:![]()
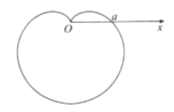
![]() 国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系
国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系![]() 中,方程
中,方程![]()
![]() 表示的曲线
表示的曲线![]() 就是一条心形线,如图,以极轴
就是一条心形线,如图,以极轴![]() 所在直线为
所在直线为![]() 轴,极点
轴,极点![]() 为坐标原点的直角坐标系
为坐标原点的直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为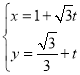 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 、
、![]() 三点,求线段
三点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 满足:(1)对任意
满足:(1)对任意![]() ,恒有
,恒有![]() 成立;(2)当
成立;(2)当![]() 时,
时,![]() .给出如下结论:
.给出如下结论:
①对任意![]() ,有
,有![]() ;
;
②函数![]() 的值域为
的值域为![]()
③存在![]() ,使得
,使得![]() ;
;
④“函数![]() 在区间
在区间![]() 上单调递减”的充要条件是“存在
上单调递减”的充要条件是“存在![]() ,使得
,使得![]() ”.
”.
上述结论正确有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000t生活垃圾.经分拣以后数据统计如下表(单位:![]() ):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
厨余垃圾”箱 | 可回收物”箱 | 其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
A.厨余垃圾投放正确的概率为![]()
B.居民生活垃圾投放错误的概率为![]()
C.该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱
D.厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com