
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF=![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=![]() .
.

(1)求证:AD⊥平面BCE;
(2)求证:AD∥平面CEF;
(3)求三棱锥A﹣CFD的体积.
【答案】(1)(2)证明见解析(3)![]()
【解析】
试题(1)依题AD⊥BD,CE⊥AD,由此能证明AD⊥平面BCE.
(2)由已知得BE=2,BD=3.从而AD∥EF,由此能证明AD∥平面CEF.
(3)由VA﹣CFD=VC﹣AFD,利用等积法能求出三棱锥A﹣CFD的体积.
(1)证明:依题AD⊥BD,
∵CE⊥平面ABD,∴CE⊥AD,
∵BD∩CE=E,
∴AD⊥平面BCE.
(2)证明:Rt△BCE中,CE=![]() ,BC=
,BC=![]() ,∴BE=2,
,∴BE=2,
Rt△ABD中,AB=2![]() ,AD=
,AD=![]() ,∴BD=3.
,∴BD=3.
∴![]() .
.
∴AD∥EF,∵AD在平面CEF外,
∴AD∥平面CEF.
(3)解:由(2)知AD∥EF,AD⊥ED,
且ED=BD﹣BE=1,
∴F到AD的距离等于E到AD的距离为1.
∴S△FAD=![]() =
=![]() .
.
∵CE⊥平面ABD,
∴VA﹣CFD=VC﹣AFD=![]() =
=![]() =
=![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣ax2﹣x;
(1)若f(x)在x=﹣1处取得极值,求a的值及f(x)的单调区间;
(2)当x>1时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点D在棱
,点D在棱![]() 上,且
上,且![]() ,建立如图所示的空间直角坐标系.
,建立如图所示的空间直角坐标系.

(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币连掷![]() 次,设事件
次,设事件![]() “恰好两次正面朝上”,
“恰好两次正面朝上”,
(1)直接计算事件![]() 的概率;
的概率;
(2)利用计算器或计算机模拟试验80次,计算事件![]() 发生的频率.
发生的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北. 湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验.在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 50 | |
个体经营户 | 50 | 150 | |
合计 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)补全上述列联表(在答题卡填写),并根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
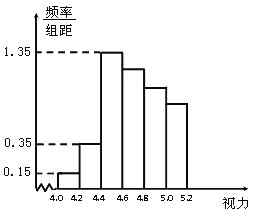

(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:

![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com