
【题目】如图所示的分数三角形,称为“莱布尼茨三角形”.这个三角形的规律是:各行中的每一个数,都等于后面一行中与它相邻的两个数之和(例如第4行第2个数 ![]() 等于第5行中的第2个数
等于第5行中的第2个数 ![]() 与第3个数
与第3个数 ![]() 之和).则
之和).则
在“莱布尼茨三角形”中,第10行从左到右第2个数到第8个数中各数的倒数之和为( )
A.5010
B.5020
C.10120
D.10130
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】对甲、乙的学习成绩进行抽样分析,各抽五门功课,得到的观测值如表:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?( )
A.甲的平均成绩较好,乙的各门功课发展较平衡
B.甲的平均成绩较好,甲的各门功课发展较平衡
C.乙的平均成绩较好,甲的各门功课发展较平衡
D.乙的平均成绩较好,乙的各门功课发展较平衡
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ ![]() (e为自然对数的底数).
(e为自然对数的底数).
(1)求函数y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈(﹣1,+∞)时,证明:f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣ ![]() x2+(a﹣1)x+lnx.
x2+(a﹣1)x+lnx.
(1)若a>﹣1,求函数f(x)的单调区间;
(2)若g(x)= ![]() x2+(1﹣2a)x+f(x)有且只有两个零点,求实数a的取值范围.
x2+(1﹣2a)x+f(x)有且只有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组数开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是 . (下列摘取了随机数表第1行至第5行) 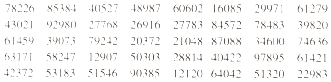
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80分为“优秀”,小于60分为“不合格”,其它为“合格”.
(1)某校高二年级有男生500人,女生400人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高二学生中抽取了90名学生的综合素质评价结果,其各个等级的频数统计如表:
等级 | 优秀 | 合格 | 不合格 |
男生(人) | 30 | x | 8 |
女生(人) | 30 | 6 | y |
根据表中统计的数据填写下面2×2列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优秀与性别有关”?
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
临界值表:
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)以(1)中抽取的90名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名学生是否“优秀”相互独立,现从该市高二学生中随机抽取4人.
(i)求所选4人中恰有3人综合素质评价为“优秀”的概率;
(ii)记X表示这4人中综合素质评价等级为“优秀”的人数,求X的数学期望.
附:参考数据与公式
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某学校组织的一次智力竞赛中,比赛共分为两个环节,其中第一环节竞赛题有A、B两组题,每个选手最多有3次答题机会,答对一道A组题得20分,答对一道B组题得30分.选手可以任意选择答题的顺序,如果前两次得分之和超过30分即停止答题,进入下一环节比赛,否则答3次.某同学正确回答A组题的概率都是p,正确回答B组题的概率都是 ![]() ,且回答正确与否相互之间没有影响.该同学选择先答一道B组题,然后都答A组题.已知第一环节比赛结束时该同学得分超过30分的概率为
,且回答正确与否相互之间没有影响.该同学选择先答一道B组题,然后都答A组题.已知第一环节比赛结束时该同学得分超过30分的概率为 ![]() .
.
(1)求p的值;
(2)用ξ表示第一环节比赛结束后该同学的总得分,求随机变量ξ的数学期望;
(3)试比较该同学选择都回答A组题与选择上述方式答题,能进入下一环节竞赛的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+2bx+c(b,c∈R).
(1)若函数y=f(x)的零点为﹣1和1,求实数b,c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(﹣3,﹣2),(0,1)内,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 个正数
个正数 ![]() 满足
满足 ![]() (
( ![]() 且
且 ![]() ).
).
(1)当 ![]() 时,证明:
时,证明: ![]() ;
;
(2)当 ![]() 时,不等式
时,不等式 ![]() 也成立,请你将其推广到
也成立,请你将其推广到 ![]() (
( ![]() 且
且 ![]() )个正数
)个正数 ![]() 的情形,归纳出一般性的结论并用数学归纳法证明.
的情形,归纳出一般性的结论并用数学归纳法证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com