
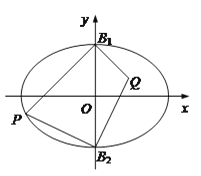
【题目】如图,在平面直角坐标系xOy中,B1,B2是椭圆![]() 的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为
的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为![]() 时,线段PB1的长为
时,线段PB1的长为![]() .
.
(1)求椭圆的标准方程;
(2)设点Q满足: ![]()
![]() .求证:△PB1B2与△QB1B2的面积之比为定值.
.求证:△PB1B2与△QB1B2的面积之比为定值.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:设![]() ,
, ![]() ,(1)根据直线
,(1)根据直线![]() 的方程为
的方程为![]() 时,线段
时,线段![]() 的长为
的长为![]() ,可分别求得
,可分别求得![]() 和
和![]() ,从而求得椭圆的标准方程;(2)方法一:直线
,从而求得椭圆的标准方程;(2)方法一:直线![]() 的斜率为
的斜率为![]() ,由
,由![]() 得直线
得直线![]() 的斜率为
的斜率为![]() ,即可分别表示出直线
,即可分别表示出直线![]() 和直线
和直线![]() 的方程,联立直线方程,得
的方程,联立直线方程,得![]() ,从而可得
,从而可得 ;方法二:设直线
;方法二:设直线![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,由
,由![]() 得直线
得直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程代入椭圆方程,从而求得
的方程代入椭圆方程,从而求得![]() ,再由
,再由![]() 在椭圆上,得
在椭圆上,得![]() 与
与![]() 的数量关系,从而表示出直线
的数量关系,从而表示出直线![]() 的方程,即可求得
的方程,即可求得![]() ,进而求得
,进而求得 .
.
试题解析:设![]() ,
, ![]() .
.
(1)在![]() 中,令
中,令![]() ,得
,得![]() ,从而b3.
,从而b3.
由 得
得![]() .
.
∴![]() .
.
∵![]()
∴![]() ,解得
,解得![]() .
.
∴椭圆的标准方程为![]() .
.
(2)方法一:
直线![]() 的斜率为
的斜率为![]() ,由
,由![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .
.
于是直线![]() 的方程为:
的方程为: ![]() .
.
同理, ![]() 的方程为:
的方程为: ![]() .
.
联立两直线方程,消去y,得![]() .
.
∵![]() 在椭圆
在椭圆![]() 上
上
∴![]() ,从而
,从而![]() .
.
∴![]() .
.
∴ .
.
方法二:
设直线![]() ,
, ![]() 的斜率为k,
的斜率为k, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由![]() 直线
直线![]() 的方程为
的方程为![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
∵![]() 是椭圆上异于点
是椭圆上异于点![]() ,
, ![]() 的点
的点
∴![]() ,从而
,从而![]()
![]() .
.
∵![]() 在椭圆
在椭圆![]() 上
上
∴![]() ,从而
,从而![]() .
.
∴![]() ,得
,得![]() .
.
由![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
联立 则
则![]() ,即
,即![]() .
.
∴ .
.


科目:高中数学 来源: 题型:
【题目】设![]() 是一个非空集合,
是一个非空集合, ![]() 是定义在
是定义在![]() 上的一个运算.如果同时满足下述四个条件:
上的一个运算.如果同时满足下述四个条件:
(1)对于![]() ,都有
,都有![]() ;
;
(2)对于![]() ,都有
,都有![]() ;
;
(3)对于![]() ,使得
,使得![]() ;
;
(4)对于![]() ,使得
,使得![]() (注:“
(注:“![]() ”同(iii)中的“
”同(iii)中的“![]() ”).
”).
则称![]() 关于运算
关于运算![]() 构成一个群.现给出下列集合和运算:
构成一个群.现给出下列集合和运算:
①![]() 是整数集合,
是整数集合, ![]() 为加法;②
为加法;②![]() 是奇数集合,
是奇数集合, ![]() 为乘法;③
为乘法;③![]() 是平面向量集合,
是平面向量集合, ![]() 为数量积运算;④
为数量积运算;④![]() 是非零复数集合,
是非零复数集合, ![]() 为乘法. 其中
为乘法. 其中![]() 关于运算
关于运算![]() 构成群的序号是___________(将你认为正确的序号都写上).
构成群的序号是___________(将你认为正确的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为优;在
以下空气质量为优;在![]() 之间空气质量为良;在
之间空气质量为良;在![]() 之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的
之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的![]() 日均值数据中随机抽取20天的数据作为样本,将
日均值数据中随机抽取20天的数据作为样本,将![]() 日均值统计如下:
日均值统计如下:
日均值( |
|
|
|
|
|
天数 | 4 | 6 | 5 | 3 | 2 |
(1)在空气质量为轻度污染的数据中,随机抽取两天![]() 日均值数据,求其中恰有一天
日均值数据,求其中恰有一天![]() 日均值数据在
日均值数据在![]() 之间的概率;
之间的概率;
(2)将以上样本数据绘制成频率分布直方图(直接作图):
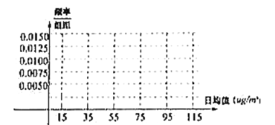
(3)该市规定:全年![]() 日均值的平均数不高于
日均值的平均数不高于![]() ,则认定该市当年的空气质量达标.现以这20天的
,则认定该市当年的空气质量达标.现以这20天的![]() 日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后他们平均每人每年创造利润为
名员工从事第三产业,调整后他们平均每人每年创造利润为![]() 万元(
万元(![]() ),剩下的员工平均每人每年创造的利润可以提高
),剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则调整员工从事第三产业的人数应在什么范围?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形CDEF是正方形,四边形ABCD为直角梯形,∠ADC=90°,AB∥DC,平面CDEF⊥平面ABCD,AB=AD![]() CD=a,M在FB上,且BD∥平面ECM.
CD=a,M在FB上,且BD∥平面ECM.

(1)求证:M为BF中点;
(2)求证:平面BCF⊥平面EMC;
(3)求直线CD与平面ECM所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com