
【题目】某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率![]() .设某商品标价为
.设某商品标价为![]() 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为![]() .
.
(Ⅰ)写出当![]() 时,
时, ![]() 关于
关于![]() 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于![]() ?
?
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的. 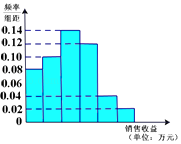
(1)根据频率分布直方图计算各小长方形的宽度;
(2)估计该公司投入4万元广告费之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值)
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
表格中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x+x,g(x)=x3+x,h(x)=log3x+x的零点依次为a,b,c,则( )
A.c<b<a
B.a<b<c
C.c<a<b
D.b<a<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 、
、![]() 、
、![]() 、
、![]() 在圆周上,
在圆周上,![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)怎样设计才能符合园林局的要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地农业监测部门统计发现:该地区近几年的生猪收购价格每四个月会重复出现,但生猪养殖成本逐月递增.下表是今年前四个月的统计情况:
月份 | 1月份 | 2月份 | 3月份 | 4月份 |
收购价格(元/斤) | 6 | 7 | 6 | 5 |
养殖成本(元/斤) | 3 | 4 | 4.6 | 5 |
现打算从以下两个函数模型:
①y=Asin(ωx+φ)+B,(A>0,ω>0,﹣π<φ<π),
②y=log2(x+a)+b
中选择适当的函数模型,分别来拟合今年生猪收购价格(元/斤)与相应月份之间的函数关系、养殖成本(元/斤)与相应月份之间的函数关系.
(1)请你选择适当的函数模型,分别求出这两个函数解析式;
(2)按照你选定的函数模型,帮助该部门分析一下,今年该地区生猪养殖户在8月和9月有没有可能亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1 , F2为椭圆 ![]() 的左右焦点,若椭圆上存在点P使得
的左右焦点,若椭圆上存在点P使得 ![]() ,则此椭圆的离心率的取值范围是( )
,则此椭圆的离心率的取值范围是( )
A.(0, ![]() )
)
B.(0, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2x﹣y+1=0,直线l2与l1关于直线y=﹣x对称,则直线l2的方程为( )
A.x﹣2y+1=0
B.x+2y+1=0
C.x﹣2y﹣1=0
D.x+2y﹣1=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com