
【题目】某班随机抽查了20名学生的数学成绩,分数制成如图的茎叶图,其中A组学生每天学习数学时间不足1个小时,B组学生每天学习数学时间达到一个小时。学校规定90分及90分以上记为优秀,75分及75分以上记为达标,75分以下记为未达标.

(1)分别求出A、B两组学生的平均分![]() 、
、![]() 并估计全班的数学平均分
并估计全班的数学平均分![]() ;
;
(2)现在从成绩优秀的学生中任意抽取2人,求这两人恰好都来自B组的概率;
(3)根据成绩得到如下列联表:

①直接写出表中![]() 的值;
的值;
②判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表:K2=![]() .
.
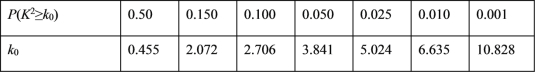
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)P(E)=
;(2)P(E)=![]() ;(3)①a=6、b=4、c=9、d=1;②没有95%的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关
;(3)①a=6、b=4、c=9、d=1;②没有95%的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关
【解析】
(1)根据平均分公式分别算出A、B两组的平均分,再根据两组的平均分估算20人的总分,估算出的平均分即为估算的班级的平均分.
(2) A组优秀人数有2人,B组优秀人数有3人.列出所有可能的基本情况,利用古典概型,即可求出结果.
(3)把数据填入表格中,利用公式求得![]() ,与临界值比较即可得出结论.
,与临界值比较即可得出结论.
(1)A组学生的平均分![]()
B两组学生的平均分![]()
估计全班的数学平均分![]()
(2)设这两人恰好都来自B组为事件![]() ,由题意该概型符合古典概型,
,由题意该概型符合古典概型,
成绩优秀的共计5人,A组2人设为![]() ,B组3人设为
,B组3人设为![]() ,
,
从5人中抽取两人有如下情况:![]()
![]()
![]()
共计包含基本事件10个,事件E包含基本事件3个
两人恰好都来自B组的概率为![]()
(3)①通过茎叶图知![]() ;
;
②由公式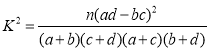 =
=![]()
![]() ,而
,而![]()
所以没有![]() 的把握认为“数学成绩达标与否”
的把握认为“数学成绩达标与否”


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】第二届中国国际进口博览会11月初在上海举行了,在这届进口博览会上,某高校派出的4人承担了连续5天的志愿者服务,若每天只安排一人且每人至少参加一天志愿服务,则甲参加2天志愿服务的概率为________(结果用数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() 设
设![]() ,若
,若![]() 为正三角形且周长为
为正三角形且周长为![]() .
.
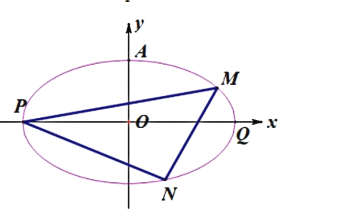
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,是否存在实数
,是否存在实数![]() 使
使![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 两点,
两点,![]() 记的面积记为
记的面积记为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 与
与![]() 满足
满足![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() 且数列
且数列![]() 为公比不为1的等比数列,求q的值,使数列
为公比不为1的等比数列,求q的值,使数列![]() 也是等比数列;
也是等比数列;
(3)若![]() 且
且![]() ,数列
,数列![]() 有最大值M与最小值
有最大值M与最小值![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,![]() 、
、![]() 为左、右焦点,焦距是实轴长的
为左、右焦点,焦距是实轴长的![]() 倍,双曲线过点
倍,双曲线过点![]() .
.
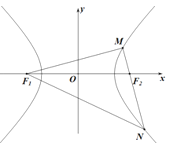
(1)求双曲线的标准方程;
(2)若点![]() 在双曲线上,求证:点
在双曲线上,求证:点![]() 在以
在以![]() 为直径的圆上;
为直径的圆上;
(3)在(2)的条件下,若直线![]() 交双曲线于另一点
交双曲线于另一点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 为数列
为数列![]() 的前
的前![]() 项和.“任意正整数
项和.“任意正整数![]() ,均有
,均有![]() ”是“
”是“![]() 为递增数列”的
为递增数列”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共有编号分别为1,2,3,4,5的五个座位,在甲同学不坐2号座位,乙同学不坐5号座位的条件下,甲、乙两位同学的座位号相加是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的长轴是短轴的两倍,点
的长轴是短轴的两倍,点![]() 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好构成等比数列.
恰好构成等比数列.
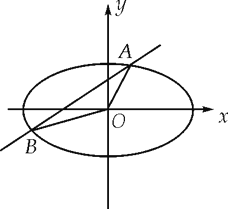
(Ⅰ)求椭圆C的方程.
(Ⅱ)试探究![]() 是否为定值?若是,求出这个值;否 则求出它的取值范围.
是否为定值?若是,求出这个值;否 则求出它的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 与
与![]() 满足
满足![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() 且数列
且数列![]() 为公比不为1的等比数列,求q的值,使数列
为公比不为1的等比数列,求q的值,使数列![]() 也是等比数列;
也是等比数列;
(3)若![]() 且
且![]() ,数列
,数列![]() 有最大值M与最小值
有最大值M与最小值![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com