
【题目】已知函数f(x)=loga(x+1),g(x)=loga(4﹣2x),a>0且a≠1.
(1)求函数y=f(x)﹣g(x)的定义域;
(2)求使不等式f(x)>g(x)成立的实数x的取值范围;
(3)求函数y=2f(x)﹣g(x)﹣f(1)的零点.
【答案】
(1)
解:y=f(x)﹣g(x)=loga(x+1)﹣loga(4﹣2x),
由题意得: ![]() ,解得:﹣1<x<2,
,解得:﹣1<x<2,
故函数的定义域是(﹣1,2)
(2)
解:不等式f(x)>g(x),
即loga(x+1)>loga(4﹣2x),
0<a<1时,x+1<4﹣2x,解得:x<1,
而﹣1<x<2,故不等式的解集是(﹣1,1);
a>1时,x+1>4﹣2x,解得:x>1,
而﹣1<x<2,故不等式的解集是(1,2);
综上,0<a<1时,不等式的解集是(﹣1,1),
a>1时,不等式的解集是(1,2)
(3)
解:令y=2f(x)﹣g(x)﹣f(1)=0,
即2loga(x+1)=loga(4﹣2x)+loga(1+1),
故(x+1)2=2(4﹣2x),解得:x=﹣7或x=1,
而﹣1<x<2,
故x=1.
【解析】(1)根据对数函数的性质求出函数的定义域即可;(2)通过讨论a的范围,得到关于x的不等式,求出不等式的解集即可;(3)令y=0,得到关于x的方程,解出即可.
【考点精析】关于本题考查的对数函数的定义域,需要了解对数函数的定义域范围:(0,+∞)才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对定义域分别为D1 , D2的函数y=f(x),y=g(x),规定:函数h(x)= 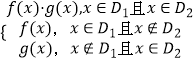 ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 .
,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.

(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?

(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,求这2人都是年龄大于40岁的概率.
附: 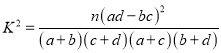 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足 ![]() ,
, ![]() .
.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较 ![]() 和ex﹣1+a哪个更靠近lnx,并说明理由.
和ex﹣1+a哪个更靠近lnx,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|f(x)=lg(x﹣1)+ ![]() },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ![]() ,求A∪B;
,求A∪B;
(2)若A∩B=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△ABC中, ![]() ,
, ![]() ,点D是BC的中点. ( I)求证:
,点D是BC的中点. ( I)求证: ![]() ;
;
( II)直线l过点D且垂直于BC,E为l上任意一点,求证: ![]() 为常数,并求该常数;
为常数,并求该常数;
( III)如图2,若 ![]() ,F为线段AD上的任意一点,求
,F为线段AD上的任意一点,求 ![]() 的范围.
的范围.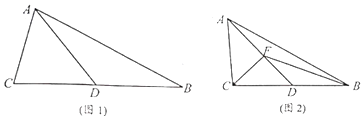
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴相邻两个交点间的距离为
)的图象与x轴相邻两个交点间的距离为 ![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥![]() ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 是正四棱锥的高
是正四棱锥的高![]() 的4倍.
的4倍.

(1)若![]() 则仓库的容积是多少?
则仓库的容积是多少?
(2)若正四棱锥的侧棱长为![]() ,则当
,则当![]() 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com