
等差数列{ },
}, =25,
=25,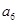 =15,数列{
=15,数列{ }的前n项和为
}的前n项和为
(1)求数列{ }和{
}和{ }的通项公式;
}的通项公式;
(2)求数列{ }的前
}的前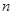 项和
项和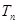 .
.
(1)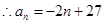 ,
,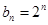 ;(2)
;(2)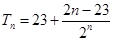 .
.
解析试题分析:(1)根据等差数列的首项和公差求通项公式;根据等比数列的首项和公比求通项公式;注意题中限制条件;(2)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用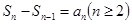 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与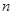 的关系,再求
的关系,再求 ;由
;由 推
推 时,别漏掉
时,别漏掉 这种情况,大部分学生好遗忘;(3)一般地,如果数列
这种情况,大部分学生好遗忘;(3)一般地,如果数列 是等差数列,
是等差数列,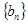 是等比数列,求数列
是等比数列,求数列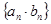 的前
的前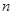 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列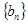 的公比,然后做差求解.
的公比,然后做差求解.
试题解析:解:(1)设等差数列 的公差为
的公差为 ,则
,则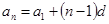
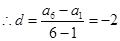 ,
,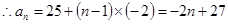
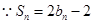 ,当
,当 时,
时,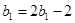 ,解得
,解得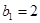
当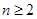 时,
时, ,即
,即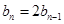
 数列
数列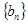 是以2为首项,公比为2的等比数列,通行公式为
是以2为首项,公比为2的等比数列,通行公式为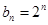
由(1)得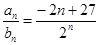
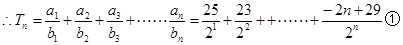
①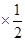 得
得 ②
②
①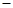 ②得
②得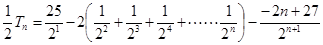
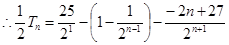
化简得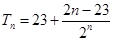
考点:(1)等差数列和等比数列的通项公式;(2)错位相减求和.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知等差数列{an}满足a3=5,a5﹣2a2=3,又等比数列{bn}中,b1=3且公比q=3.
(1)求数列{an},{bn}的通项公式;
(2)若cn=an+bn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列 满足:
满足: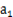 =2,且
=2,且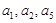 成等比数列.
成等比数列.
(1)求数列 的通项公式.
的通项公式.
(2)记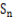 为数列
为数列 的前n项和,是否存在正整数n,使得
的前n项和,是否存在正整数n,使得 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
打一口深20米的井,打到第一米深处时需要40分钟,从第一米深处打到第二米深处需要50分钟,以后每深一米都要比前一米多10分钟,则打到最后一米深处要用 小时,打完这口井总共用 小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com