解:(1)k=0时,f(x)=ex-x,
f'(x)=ex-1.
当x∈(-∞,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0.
所以f(x)在(-∞,0)上单调减小,在(0,+∞)上单调增加
故f(x)的最小值为f(0)=1
(2)f'(x)=ex-kx-1,
f''(x)=ex-k
当k≤1时,f''(x)≥0(x≥0),
所以f'(x)在[0,+∞)上递增,
而f'(0)=0,
所以f'(x)≥0(x≥0),
所以f(x)在[0,+∞)上递增,
而f(0)=1,
于是当x≥0时,f(x)≥1.
当k>1时,
由f''(x)=0得x=lnk
当x∈(0,lnk)时,f''(x)<0,所以f'(x)在(0,lnk)上递减,
而f'(0)=0,于是当x∈(0,lnk)时,f'(x)<0,所以f(x)在(0,lnk)上递减,
而f(0)=1,所以当x∈(0,lnk)时,f(x)<1.
综上得k的取值范围为(-∞,1].
分析:(1)将k的值代入f(x),求出f(x)的导函数,令导函数大于0求出函数的单调递增区间,令导函数小于0求出函数的单调递减区间,求出函数的最小值.
(2)求出f(x)的导函数,再求出导函数的导数,通过对k的讨论,判断出二阶导数的符号,判断出f(x)的导函数的最值,从而判断出导函数的符号,得到f(x)的单调性,求出f(x)的最小值,令最小值大于1,列出不等式求出k的范围.
点评:本题考查导数在最大值与最小值问题中的应用,解题的关键是利用导数研究出函数的单调性,判断出函数的最值,本题第二小题是一个恒成立的问题,恒成立的问题一般转化最值问题来求解,本题即转化为用单调性求函数在闭区间上的最值的问题,求出最值再判断出参数的取值.

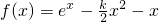 .
.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案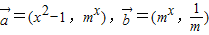 ,设函数
,设函数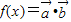 .
.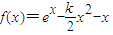 .
.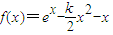 .
.