
【题目】设函数f(x)=ax2–a–lnx,g(x)=![]() ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)证明:当x>1时,g(x)>0;
(Ⅲ)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
【答案】(Ⅰ)当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;当
单调递减;当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增;(Ⅱ)详见解析;(Ⅲ)
单调递增;(Ⅱ)详见解析;(Ⅲ)![]()
![]() .
.
【解析】
试题本题考查导数的计算、利用导数求函数的单调性,解决恒成立问题,考查学生的分析问题、解决问题的能力和计算能力.第(Ⅰ)问,对![]() 求导,再对a进行讨论,判断函数的单调性;第(Ⅱ)问,利用导数判断函数的单调性,从而证明结论,第(Ⅲ)问,构造函数
求导,再对a进行讨论,判断函数的单调性;第(Ⅱ)问,利用导数判断函数的单调性,从而证明结论,第(Ⅲ)问,构造函数![]() =
=![]()
![]()
![]() (
(![]() ),利用导数判断函数
),利用导数判断函数![]() 的单调性,从而求解a的值.
的单调性,从而求解a的值.
试题解析:(Ⅰ)![]()
![]()
![]() <0,
<0,![]() 在
在![]() 内单调递减.
内单调递减.
![]() 由
由![]() =0有
=0有![]() .
.
当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;
单调递减;
当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增.
单调递增.
(Ⅱ)令![]() =
=![]() ,则
,则![]() =
=![]() .
.
当![]() 时,
时,![]() >0,所以
>0,所以![]() ,从而
,从而![]() =
=![]() >0.
>0.
(Ⅲ)由(Ⅱ),当![]() 时,
时,![]() >0.
>0.
当![]() ,
,![]() 时,
时,![]() =
=![]() .
.
故当![]() >
>![]() 在区间
在区间![]() 内恒成立时,必有
内恒成立时,必有![]() .
.
当![]() 时,
时,![]() >1.
>1.
由(Ⅰ)有![]() ,而
,而![]() ,
,
所以此时![]() >
>![]() 在区间
在区间![]() 内不恒成立.
内不恒成立.
当![]() 时,令
时,令![]() =
=![]()
![]()
![]() (
(![]() ).
).
当![]() 时,
时,![]() =
=![]()
![]() .
.
因此,![]() 在区间
在区间![]() 单调递增.
单调递增.
又因为![]() =0,所以当
=0,所以当![]() 时,
时,![]() =
=![]()
![]()
![]() >0,即
>0,即![]() >
>![]() 恒成立.
恒成立.
综上,![]()
![]() .
.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
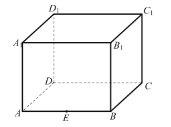
【题目】在正方形![]() 中,
中,![]() ,
,![]() 分别为棱
分别为棱![]() 和棱
和棱![]() 的中点,则下列说法正确的是( )
的中点,则下列说法正确的是( )
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() 截正方体所得截面为等腰梯形
截正方体所得截面为等腰梯形
C.![]() 平面
平面![]() D.异面直线
D.异面直线![]() 与
与![]() 所成的角为60°
所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长
的底面边长![]() ,侧棱长
,侧棱长![]() ,它的外接球的球心为
,它的外接球的球心为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是球
是球![]() 上的任意一点,有以下命题:
上的任意一点,有以下命题:
①![]() 的长的最大值为9;
的长的最大值为9;
②三棱锥![]() 的体积的最大值是
的体积的最大值是![]() ;
;
③存在过点![]() 的平面,截球
的平面,截球![]() 的截面面积为
的截面面积为![]() ;
;
④三棱锥![]() 的体积的最大值为20;
的体积的最大值为20;
⑤过点![]() 的平面截球
的平面截球![]() 所得的截面面积最大时,
所得的截面面积最大时,![]() 垂直于该截面.
垂直于该截面.
其中是真命题的序号是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了![]() 个网箱,测量各水箱产品的产量(单位:kg),其频率分布直方图如下图所示.
个网箱,测量各水箱产品的产量(单位:kg),其频率分布直方图如下图所示.

(1)若用频率视为概率,记![]() 表示事件“旧养殖法的箱产量低于
表示事件“旧养殖法的箱产量低于![]() kg”,求事件
kg”,求事件![]() 的概率;
的概率;
(2)填写以下![]() 列联表,并根据此判断是否有
列联表,并根据此判断是否有![]() 的把握认为箱产量与养殖方法有关?
的把握认为箱产量与养殖方法有关?
箱产量 | 箱产量 | 合计 | |
旧养殖方法 | |||
新养殖方法 | |||
合计 |
(3)根据箱产量频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知i为虚数单位,下列说法中正确的是( )
A.若复数z满足![]() ,则复数z对应的点在以
,则复数z对应的点在以![]() 为圆心,
为圆心,![]() 为半径的圆上
为半径的圆上
B.若复数z满足![]() ,则复数
,则复数![]()
C.复数的模实质上就是复平面内复数对应的点到原点的距离,也就是复数对应的向量的模
D.复数![]() 对应的向量为
对应的向量为![]() ,复数
,复数![]() 对应的向量为
对应的向量为![]() ,若
,若![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号、33号、46号同学在样本中,那么样本中另一位同学的编号为23;
②一组数据1,2,3,3,4,5的平均数、众数、中位数都相同;
③一组数据![]() ,0,1,2,3,若该组数据的平均值为1,则样本的标准差为2;
,0,1,2,3,若该组数据的平均值为1,则样本的标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中真命题为( )
A.①②④B.②④C.②③④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,求实数a,b的值;
,求实数a,b的值;
(2)若![]() ,求
,求![]() 的单调减区间;
的单调减区间;
(3)对一切实数![]() ,求
,求![]() 的极小值函数
的极小值函数![]() ,并求出
,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的首项为0,公差为a,
的首项为0,公差为a,![]() ;等差数列
;等差数列![]() 的首项为0,公差为b,
的首项为0,公差为b,![]() .由数列
.由数列![]() 和
和![]() 构造数表M,与数表
构造数表M,与数表![]() ;
;
记数表M中位于第i行第j列的元素为![]() ,其中
,其中![]() ,(i,j=1,2,3,…).
,(i,j=1,2,3,…).
记数表![]() 中位于第i行第j列的元素为
中位于第i行第j列的元素为![]() ,其中
,其中![]() (
(![]() ,
,![]() ,
,![]() ).如:
).如:![]() ,
,![]() .
.
(1)设![]() ,
,![]() ,请计算
,请计算![]() ,
,![]() ,
,![]() ;
;
(2)设![]() ,
,![]() ,试求
,试求![]() ,
,![]() 的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于数表
的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于数表![]() ;
;
(3)设![]() ,
,![]() ,对于整数t,t不属于数表M,求t的最大值.
,对于整数t,t不属于数表M,求t的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com