
【题目】下列四个命题:
①函数![]() 是奇函数且在定义域上是单调递增函数;
是奇函数且在定义域上是单调递增函数;
②函数![]() 有两个零点,则
有两个零点,则![]() ;
;
③函数![]() ,则
,则![]() 的解集为
的解集为![]() ;
;
④函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
其中正确命题的序号为__________.
【答案】③
【解析】
根据正切函数性质,判断①错误;根据指数函数翻折变换画图,根据图像即可求解参数取值范围,知②错;根据函数解析式判断函数单调性及奇偶性,即可求解集,知③正确;根据复合函数单调性法则,求解单调区间,知④错误.
对于①,正切函数![]() 是奇函数,定义域为
是奇函数,定义域为![]() ,单调区间为
,单调区间为![]() ,在每一个区间内单调递增,但不是在其定义域内单调递增,故①错误;
,在每一个区间内单调递增,但不是在其定义域内单调递增,故①错误;
对于②,函数![]() 有两个零点,转化成
有两个零点,转化成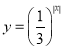 与直线
与直线![]() 有两个交点,作两个函数图象,如下图所示:
有两个交点,作两个函数图象,如下图所示:

根据图像,可知![]() ,故②错误;
,故②错误;
对于③,函数![]() ,
,![]() 是奇函数,
是奇函数,

![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,
上单调递增,
由![]() ,则
,则![]()
![]() ,解得
,解得![]()
则解集为![]() ,故③正确;
,故③正确;
对于④,函数![]() 是复合函数,令
是复合函数,令![]() 是内层函数,
是内层函数,![]() 是外层函数,根据复合函数单调性同增异减,
是外层函数,根据复合函数单调性同增异减,![]() 在
在![]() 是增函数,则
是增函数,则![]() 为减函数,又
为减函数,又![]() ,则减区间为
,则减区间为![]() ,故④错误;
,故④错误;
故答案为:③


科目:高中数学 来源: 题型:
【题目】如图所示,某镇有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() ,
,![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.

(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左
的左![]() 、
、![]() 右焦点分别为,点
右焦点分别为,点![]() 在椭圆上,且满足
在椭圆上,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设倾斜角为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,求
,求![]() 取最大值时直线
取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]()
(1)若函数在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)是否存在常数![]() ,当
,当![]() 时,
时,![]() 的值域为区间
的值域为区间![]() ,且区间
,且区间![]() 的长度为
的长度为![]() (视区间
(视区间![]() 的长度为
的长度为![]() ),如果存在,求出
),如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2表示没有击中目标,3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20随机数:![]()
![]()
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A.0.55B.0.6C.0.65D.0.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com