
【题目】已知平面向量![]() ,设函数
,设函数![]() (
(![]() 为常数且满足
为常数且满足![]() ),若函数
),若函数![]() 图象的一条对称轴是直线
图象的一条对称轴是直线![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的最大值和最小值:
上的最大值和最小值:
(3)证明:直线![]() 与函数
与函数![]() 的图象不相切.
的图象不相切.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
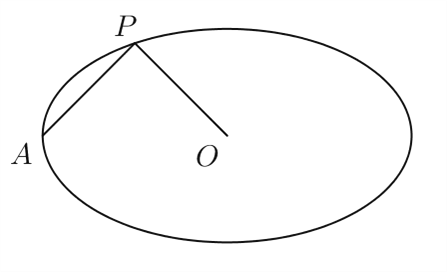
【题目】嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为![]() 公里,远月点与月球表面距离为
公里,远月点与月球表面距离为![]() 公里.已知月球的直径为
公里.已知月球的直径为![]() 公里,则该椭圆形轨道的离心率约为
公里,则该椭圆形轨道的离心率约为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() ABCD中,
ABCD中,![]() 和
和![]() 都是等边三角形,平面PAD
都是等边三角形,平面PAD![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .
.
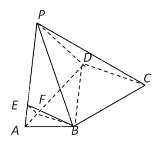
(1)求证:CD![]() PA;
PA;
(2)E,F分别是棱PA,AD上的点,当平面BEF//平面PCD时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆M:![]() 的左顶点为
的左顶点为![]() 、中心为
、中心为![]() ,若椭圆M过点
,若椭圆M过点![]() ,且
,且![]()
![]() .
.
(1)求椭圆M的方程;
(2)若△APQ的顶点Q也在椭圆M上,试求△APQ面积的最大值;
(3)过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交椭圆M于
的直线交椭圆M于![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 恒过一个定点.
恒过一个定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com