已知点F(0,1),直线l:y=-2.
(1)若动点M到点F的距离比它到直线l的距离小1,求动点M的轨迹E的方程;
(2)过轨迹E上一点P作圆C:x2+(y-3)2=1的切线,切点分别为A、B,求四边形PACB的面积S的最小值和此时P的坐标.
【答案】
分析:(1)直接代入距离公式来求动点M轨迹E的方程即可(注意讨论).
(2)先利用图象和已知条件把S转化为求|AP|问题,然后在△PAC中借助于点P在E上求出|AP|的最小值即可.
解答:解:(1):设动点M(x,y).
由题设条件可知

,即

①当y+2≥0时,即y≥-2时,有

两端平方并整理得

②当y+2<0即y<-2时有

两端平方并整理得

∵x
2>0∴

>-1
这与y<-2矛盾.
综合①②知轨迹E的方程为

(2)连PC,不难发现S=S
△PAC+S
△PBC=2S
△PAC∵CA⊥PA且|AC|=1∴
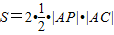
即S=|AP||
设P(x
,y
)于是,|AP|
2+|AC|
2=|PC|
2=x
2+(y
-3)
2即

∴
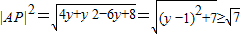
当且仅当y
=1时“=”成立,此时x
=±2
所以四边形PACB存在最小值,最小值是

,此时P点坐标是(±2,1)
点评:本题以轨迹方程为载体,考查到求动点M的轨迹E的方程问题.在做这一类型题时,关键是找到关于动点M的等式.

 ,即
,即 




 >-1
>-1
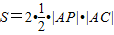

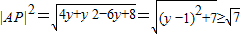
 ,此时P点坐标是(±2,1)
,此时P点坐标是(±2,1)

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案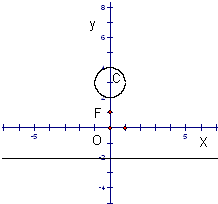 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1. (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且